Одна и та же сила может сообщать вращающемуся телу разные угловые ускорения в зависимости от её направления и точки приложения. Для характеристики вращающего действия силы вводят понятие момента силы.
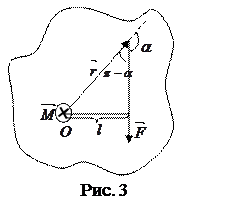Различают момент силы относительно неподвижной точки и относительно неподвижной оси. Моментом силы относительно точки О (полюса) называется векторная величина, равная векторному произведению радиус-вектора 
проведенного из точки О в точку приложения силы, на вектор силы: 
.
Поясняющий это определение рис. 3 выполнен в предположении, что точка О и вектор 
лежат в плоскости чертежа, тогда вектор 
также располагается в этой плоскости, а вектор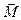 
^ к ней и направлен от нас (как векторное произведение 2-х векторов; по правилу правого буравчика). 
Модуль момента силы численно равен произведению силы на плечо:
,
где 
- плечо силы относительно точки О, a - угол между направлениями и , 
.
Плечо - кратчайшее расстояние от центра вращения до линии действия силы.
Вектор момента силы сонаправлен с поступательным движением правого буравчика, если его рукоятку вращать по направлению вращающего действия силы. Момент силы - аксиальный (свободный) вектор, он направлен вдоль оси вращения, не связан с определенной линией действия, его можно переносить в
пространстве параллельно самому себе.
Моментом силы относительно неподвижной оси Z называется проекция вектора 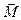на эту ось (проходящую через точку О):
.
Если на тело действуют несколько сил, то результирующий момент сил относительно неподвижной оси Z равен алгебраической сумме моментов всех сил относительно этой оси.
Если сила, приложенная к телу, не лежит в плоскости вращения, её можно разложить на 2 компоненты: лежащую в плоскости вращения 
и перпендикулярную к ней Fn. Как видно из рисунка 4, Fn вращения не создает, а приводит только к деформации тела; вращение тела обусловлено только составляющей Ft.
