| Задание 1. Найти интеграл, используя таблицу и основные свойства неопределённого интеграла. | |
| 1. | 
|
| Задание 2–3. Найти интеграл, используя подходящую подстановку. | |
| 2. | 
|
| 3. | 
|
| Задание 4–6. Найти интеграл, используя метод интегрирования по частям. | |
| 4. | 
|
| 5. |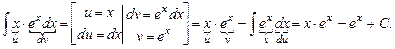 
|
| 6. | 
Итак, имеем:  .
Перенося интеграл из правой части равенства в левую, получаем:
 
и окончательно имеем 
|
| Задание 7–11. Найти интегралы от простейших рациональных дробей. | |
| 7. | 
|
| 8. | 
|
| 9. | 
|
| 10. | |
| 11. | |
| 12. | |
| Задание 13–15. Найти интегралы от тригонометрических функций. | |
| 13. | 
|
| 14. | |
| 15. | 
|
КОНТРОЛЬНАЯ РАБОТА №5
Задание 1. Исследовать сходимость числовых рядов:
а) используя признак сравнения; б) по признаку Даламбера;
Задание 2. Исследовать ряд на условную и абсолютную сходимость;
Задание 3. Найти область сходимости степенного ряда.
| Задание 1 | Задание 2 | Задание 3 | ||
| 
| 
| 
| |
| 
| 
| 
| |
| 
| 
| 
| |
| 
| 
| 
| |
| 
| 
| 
| |
| 
| 
| 
| |
| 
| 
| 
| |
| 
| 
| 
| |
| 
| 
| 
| |
| 
| 
| 
|
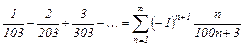
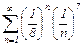
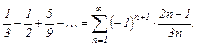
КОНТРОЛЬНЫЕ ВОПРОСЫ К ЭКЗАМЕНУ
| 1. | Как определяется десятая частичная сумма числового ряда? |
| 2. | Как определяется сумма числового ряда? Какой ряд называется сходящимся? |
| 3. | При каком  обобщенный гармонический ряд является сходящимся?
|
| 4. | Каким будет предел общего члена сходящегося числового ряда? |
| 5. | Какие ряды выбираются в качестве эталонных при использовании признака сравнения? |
| 6. | Будет ли сходящимся ряд с положительными членами, для которого предел отношения последующего члена к предыдущему члену равен 2? |
| 7. | Предел какого выражения используется в признаке Каши? |
| 8. | Какой ряд называется знакопеременным? Какой ряд называется знакочередующимся? |
| 9. | Будет ли сходящимся знакопеременный ряд, для которого ряд из модулей его членов сходится? |
| 10. | Какой ряд называется абсолютно сходящимся? Какой ряд называется условно сходящимся? |
| 11. | Каких условий достаточно для сходимости знакочередующегося ряда? |
| 12. | Как называется множество всех  , при которых степенной ряд сходится?
|
| 13. | Что такое радиус сходимости степенного ряда? По какой формуле находится радиус? |
| 14. | Для какой функции можно определить ряд Тейлора? Как из ряда Тейлора можно получить ряд Маклорена? |
