Задание 1. Найти производные функций.
Задание 2. Вычислить приближённо.
Задание 3. Исследовать функции и построить её график.
| № | Задание 1. | Задание 2. | Задание 3. | ||
| 11. | 
| 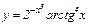
| 
| 
| 
|
| 12. | 
| 
| 
| 
| 
|
| 13. | 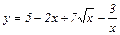
| 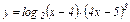
| 
| 
| 
|
| 14. | 
| 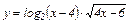
| 
| 
| 
|
| 15. | 
| 
| 
| 
| 
|
| 16. | 
| 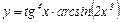
| 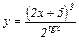
| 
| 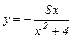
|
| 17. | 
| 
| 
| 
| 
|
| 18. | 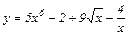
| 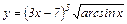
| 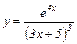
| 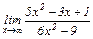
| 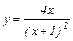
|
| 19. | 
| 
| 
| 
| 
|
| 20. | 
| 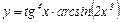
| 
| 
| 
|
КОНТРОЛЬНЫЕ ВОПРОСЫ К ЭКЗАМЕНУ
| 17. | Понятие производной. |
| 18. | Производная основных элементарных функций. |
| 19. | Правила дифференцирования. |
| 20. | Геометрический смысл производной. |
| 21. | Производные высших порядков. |
| 22. | Производная сложной функции. |
| 23. | Условия монотонности функции. |
| 24. | Экстремумы функции. |
| 25. | Выпуклость графика функции. Точки перегиба. |
| 26. | Асимптоты графика функции. |
| 27. | Общая схема исследования функции и построения графика. |
КОНТРОЛЬНАЯ РАБОТА №4
Задание 1. Найти интеграл, используя таблицу и основные свойства неопределённого интеграла.
Задание 2–3. Найти интеграл, используя подходящую подстановку.
Задание 4–6. Найти интеграл, используя метод интегрирования по частям.
Задание 7–11. Найти интегралы от простейших рациональных дробей.
Задание 12. Найти интегралы от иррациональных функций.
Задание 13–15. Найти интегралы от тригонометрических функций.
| Вариант № 1 | Вариант № 2 | Вариант № 3 | Вариант № 4 | Вариант № 5 | |

| 
| 
| 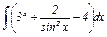
| 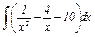
| |

| 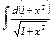
| 
| 
| 
| |
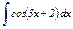
| 
| 
| 
| 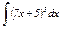
| |
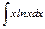
| 
| 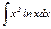
| 
| 
| |
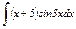
| 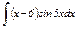
| 
| 
| 
| |

| 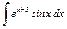
| 
| 
| 
| |

| 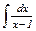
| 
| 
| 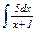
| |

| 
| 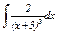
| 
| 
| |

| 
| 
| 
| 
| |

| 
| 
| 
| 
| |

| 
| 
| 
| 
| |

| 
| 
| 
| 
| |

| 
| 
| 
| 
| |
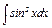
| 
| 
| 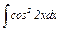
| 
| |

| 
| 
| 
| 
|
| Вариант № 6 | Вариант № 7 | Вариант № 8 | Вариант № 9 | Вариант № 10 | |

| 
| 
| 
| 
| |

| 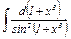
| 
| 
| 
| |
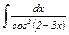
| 
| 
| 
| 
| |

| 
| 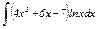
| 
| 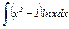
| |
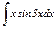
| 
| 
| 
| 
| |

| 
| 
| 
| 
| |

| 
| 
| 
| 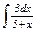
| |

| 
| 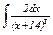
| 
| 
| |

| 
| 
| 
| 
| |

| 
| 
| 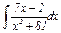
| 
| |
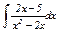
| 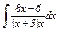
| 
| 
| 
| |

| 
| 
| 
| 
| |

| 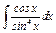
| 
| 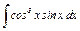
| 
| |

| 
| 
| 
| 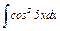
| |

| 
| 
| 
| 
|
КОНТРОЛЬНЫЕ ВОПРОСЫ К ЭКЗАМЕНУ
| 1. | Понятие первообразной и неопределённого интеграла. |
| 2. | Основные свойства неопределённого интеграла. |
| 3. | Интегралы от основных элементарных функций. |
| 4. | Основные методы интегрирования. Непосредственное интегрирование. |
| 5. | Основные методы интегрирования. Интегрирование методом замены. |
| 6. | Основные методы интегрирования. Интегрирование по частям. |
| 7. | Интегрирование рациональных дробей. |
| 8. | Интегрирование простейших иррациональных дробей. |
| 9. | Интегрирование тригонометрических функций. |
| 10. | Понятие определённого интеграла. Формула Ньютона – Лейбница. |
| 11. | Основные свойства определённого интеграла. |
| 12. | Основные методы вычисление определённого интеграла. Формула Ньютона – Лейбница. |
| 13. | Геометрические приложения определённого интеграла. Вычисление площадей плоских фигур. |
| 14. | Геометрические приложения определённого интеграла. Вычисление объёмов тел вращения. |






