Встановлення закономірностей, яким підпорядковані масові випадкові явища, засноване на вивченні теорії ймовірностей статистичних даних – результатів спостережень.
Перше завдання математичної статистики – вказати способи збору та угруповання статистичних відомостей, отриманих в результаті спостережень чи в результаті спеціально поставлених експериментів.
Друге завдання математичної статистики – розробляти методи аналізу статистичних даних в залежності від мети досліджень.
Центральним поняттям статистики є поняття статистичної сукупності, як маси деяких однорідних елементів, що відрізняються між собою за певними ознаками. Одиниці сукупності, з яких складається статистична сукупність, надалі будемо називати елементами цієї сукупності (на практиці – варіантами або ознаками).
Встановлення статистичних закономірностей, щодо масових випадкових явищ, грунтується на вивченні статистичних даних – відомостей про те, які значення прийняла окрема ознака (випадкова величина Х) унаслідок проведення досліду.
На практиці статистичних досліджень відрізняють два види дослідів:
- суцільний, коли розглядаються всі елементи сукупності;
- вибірковий, де вивчається лише деяка частина елементів.
Вся сукупність елементів, яку треба вивчити називається генеральною сукупністю. Та частина об’єктів, що її відібрано для безпосереднього вивчення із генеральної сукупності, називається вибірковою сукупністю (або просто – вибіркою). Кількість елементів у генеральній чи вибірковій сукупності називають їх об’ємами.
Генеральна сукупність може мати, як скінчений так і нескінчений об’єм. Вибіркова сукупність розглядається, як деякий емпіричний аналог генеральної сукупності. Сутність вибіркового методу полягає в тому, щоб за деякою частиною генеральної сукупності (за вибіркою) робити висновки про її властивості в цілому, наприклад, про її закон розподілу, або про числові значення її певних параметрів. Головним недоліком вибіркового методу є помилки досліду, які також називають помилками репрезентативності.
Щоб за даними вибірки мати можливість судити про генеральну сукупність, вона повинна бути взята випадково, це у певній мірі дозволяє знизити можливість помилок репрезентативності. Випадковість елементів у вибірці досягається шляхом слідування принципу рівної можливості всіх елементів генеральної сукупності бути відібраними у вибірку. Вибіркову сукупність називають репрезентативною, якщо вона досить добре відбиває основні характеристики генеральної сукупності.
Розрізняють наступні види вибірок:
- власне-випадкова вибірка, отримана випадковим відбором елементів без поділу їх на частини або групи;
- механічна вибірка, для якої елементи генеральної сукупності відбираються через деякий інтервал;
- типова вибірка, у яку випадковим чином вибираються елементи з типових груп, на які за деякою ознакою поділяється генеральна сукупність;
- серійна вибірка, у яку випадковим чином потрапляють не елементи груп, а власне групи, які потім суцільно досліджуються.
Для вивчення генеральної сукупності відносно кількісної ознаки Х вилучена вибірка об’єму 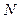 .
.
Вибірковою середньою 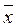 називають середнє арифметичне значення вибіркової сукупності
називають середнє арифметичне значення вибіркової сукупності 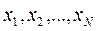
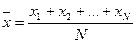 . (1)
. (1)
Але для того, щоб дати якісну характеристику значень кількісної ознаки Х генеральної сукупності навколо свого середнього значення, вводять ще одну зведену характеристику – вибіркову дисперсію (D), як називається середнє арифметичне квадратів відхилень значень ознаки генеральної сукупності від їх середнього значення 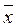
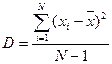 . (2)
. (2)
Окрім дисперсії для характеристики розсіювання значень ознаки генеральної сукупності навколо свого середнього значення користуються зведеною характеристикою – середнім квадратичним відхиленням (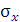 )
)
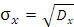 . (3)
. (3)
Раніше ми розглядали ситуації, коли під час експерименту досліджувалась одна якась ознака (випадкова величина). Інші наявні у досліджуваної сукупності ознаки або вважалися сталими, або відносилися до випадкових факторів, які впливають на зміни ознаки, яка вивчалася. Але, насправді, статистичні дослідження значно складніші і виникає питання про взаємозв’язок (залежність) між окремими випадковими величинами.
Зв’язки (залежності) між різними явищами навколишнього середовища складні і багатогранні, але при математичному моделюванні ці зв’язки можна певним способом класифікувати як функціональні та стохастичні.
Суть функціонального зв’язку полягає в тому, що деяка величина визначається як однозначна функція однієї або декількох величин. Для випадкових величин строго функціональний зв’язок реалізується рідко. Це пов’язано з тим, що в системі (X,Y) обидві величини або одна з них зазнають впливу випадкових факторів. Більш того, серед цих факторів можуть бути і спільні, тобто такі, які впливають на обидві величини одночасно.
В тих випадках, коли зв’язок між випадковими величинами втрачає функціональний характер і досліджуваний об’єкт або система об’єктів переходить не в однозначно визначений стан, а в один з можливих станів, має місце так званий стохастичний зв’язок. Суть стохастичного зв’язку полягає в тому, що із зміни однієї випадкової величини випливає зміна закону розподілу другої.
В практиці статистичних досліджень часто розглядається окремий випадок стохастичного зв’язку, який називається статистичним зв’язком. Про цей зв’язок можна говорити тоді, коли умовне математичне сподівання однієї випадкової величини Y, є функцією значення, якого набуває друга випадкова величинa X. Таким чином, щоб вивчати статистичний зв’язок, потрібно знати умовне математичне сподівання. Для його оцінки необхідно знати закон розподілу двовимірної випадкової величини 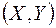 .
.
Метод статистичного аналізу для дослідження і оцінки залежностей між випадковими величинами за відповідними коефіцієнтами кореляції називається кореляційним аналізом. Кореляційний аналіз оцінює, наскільки значні невипадкові зміни у випадкових величинах у процесі проведення експерименту. Кореляційний аналіздосліджує наявність і характер зв’язків між випадковими величинами Х і Y.
З теорії ймовірності відомо, що ступінь зв’язку між випадковими величинами Х і Y визначається такими числовими характеристиками їхнього сумісного розподілу як коефіцієнт кореляції (r)
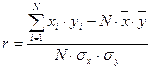 , (4)
, (4)
де 
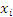 ,
, 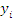 - значення варіант випадкових величин Х і Y;
- значення варіант випадкових величин Х і Y;
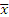 ,
, 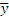 - середнє арифметичне випадкових величин Х і Y;
- середнє арифметичне випадкових величин Х і Y;
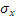 ,
, 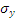 - середнє квадратичне відхилення випадкових величин Х і Y.
- середнє квадратичне відхилення випадкових величин Х і Y.
Вибірковий коефіцієнт кореляції характеризує зв’язок між випадковими величинами Х і Y за наступними характеристиками:
а) якщо 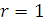 , то зв’язок між Х і Y є ідеальною функціональною залежністю;
, то зв’язок між Х і Y є ідеальною функціональною залежністю;
б) якщо 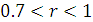 , то зв’язок між Х і Y є дуже сильним;
, то зв’язок між Х і Y є дуже сильним;
в) якщо 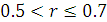 , то зв’язок між Х і Y є сильним;
, то зв’язок між Х і Y є сильним;
г) якщо 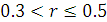 , то зв’язок між Х і Y є середнім;
, то зв’язок між Х і Y є середнім;
д) якщо 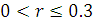 , то зв’язок між Х і Y є слабким;
, то зв’язок між Х і Y є слабким;
е) якщо 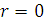 , то випадкові величини Х і Y є некорельовані і це означає лише відсутність лінійного зв’язку між ними.
, то випадкові величини Х і Y є некорельовані і це означає лише відсутність лінійного зв’язку між ними.
Вибірковий коефіцієнт кореляції задовольняє нерівність 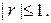
Перш ніж використати формули (1) – (4) необхідно пронормувати випадкові величини Х і Y. Нормування доцільно виконати за формулами
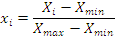 , (5)
, (5)
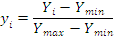 , (6)
, (6)
де 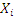 ,
, 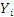 – значення випадкової величини Х і Y відповідно;
– значення випадкової величини Х і Y відповідно;
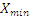 ,
, 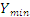 - мінімальне значення випадкової величини Х і Y відповідно;
- мінімальне значення випадкової величини Х і Y відповідно;
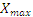 ,
, 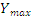 - максимальне значення випадкової величини Х і Y відповідно.
- максимальне значення випадкової величини Х і Y відповідно.
Таким чином, послідовність кореляційного аналізу така:
1. Сформувати таблицю статистичних даних з додатків, які вказані у завданні (у формі табл. А.1)
Таблиця А.1.
| Рік | … | |||
| Значення i | … | N | ||
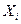
| … | |||
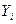
| … |
2. Пронормувати випадкові величини відповідно формул (5), (6) та заповнити табл. А.2.
Таблиця А.2.
| Рік | … | |||
| Значення i | … | N | ||
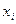
| … | |||
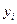
| … |
3. Вичислити середньо арифметичні 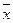 та
та 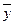 відповідно рівнянню (1).
відповідно рівнянню (1).
4. Вичислити середньо квадратичні відхилення 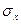 ,
, 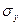 відповідно рівнянням (2), (3).
відповідно рівнянням (2), (3).
5. Вичислити коефіцієнт кореляції відповідно (4).
6. Проаналізувати ступінь кореляційного зв’язку та зробити висновок.
Додаток Б.
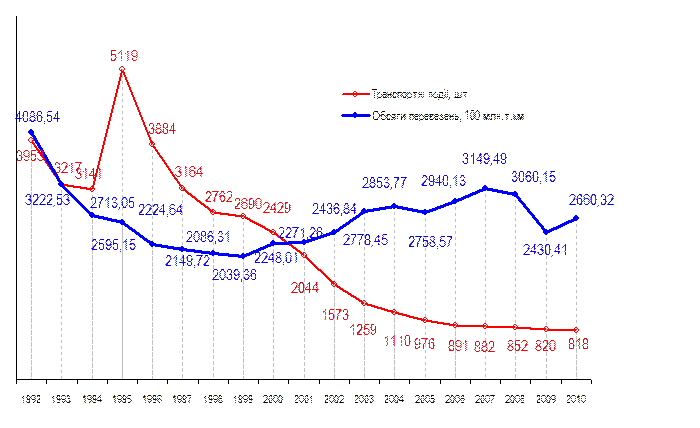
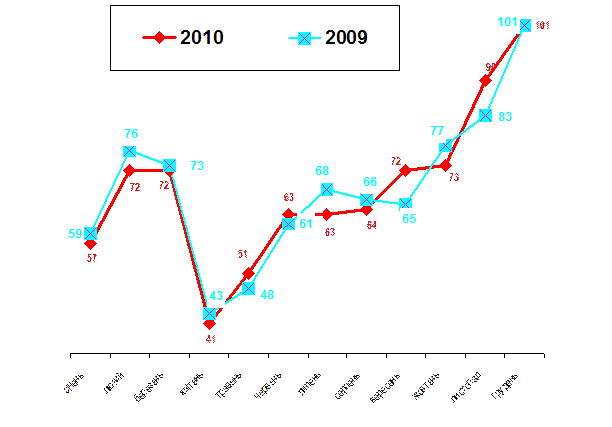
Динаміка кількості транспортних подій у відношенні до обсягів перевезень
· Кількість транспортних подій допущених по місяцях у 2010/2009 роках
Додаток В.






