КЕРЧЕНСКИЙ ГОСУДАРСТВЕННЫЙ МОРСКОЙ ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ
ИНФОРМАТИКА
Задания к контрольной работе
Для студентов–заочников специальностей
7.100304 "Судовождение",
Quot;Технологія хранения, консервирования и переработки
рыбы и морепродуктов"
Белгород-Днестровского учебно-консультационного центра КМТИ
Керчь
УДК 681.3;338.984
| Авторы: | Ершов М.Н.,к.т.н., доцент кафедры информатики и прикладной математики Керченского морского технологического института. Сикерина Н.В., ст. преподаватель кафедры информатики и прикладной математики Керченского морского технологического института. |
| Рецензенты: | Ильин Б.В., к.т.н., зав. кафедрой информатики и прикладной математики Керченского морского технологического института. Полупанов В.Н., к.т.н., директор фирмы «Эликон». |
Методические указания рассмотрены и одобрены на заседании кафедры информатики и прикладной математики КМТИ, протокол № 7 от 20.03.2004.
Методические указания рассмотрены и одобрены на ученом совете КМТИ, протокол № 8 от 24.04.2004.
©Керченский морской технологический институт, 2004
Общие организационно-методические указания
Раздел "Численные методы решения задач" дисциплины “Информатика” для специальностей 7.100304, 7.091708 рассчитан на 2 семестра. В 1-м студенты изучают теоретический курс, выполняют контрольную работу №3 и сдают экзамен, во 2-м выполняют заключительную курсовую работу.
Вычислительная часть контрольной работы выполняется в среде Excel. Отчет по контрольной работе оформляется в установленном порядке и должен по каждому из 5 заданий содержать:
1. ответы на контрольные вопросы;
2. формулировку задания с указанием данных, выбранных из таблицы вариантов;
3. EXCEL-файл решения задачи (представляется на дискете);
4. результаты решения задачи.
Примеры выполнения заданий контрольной работы №3, а также перечень необходимой учебной литературы представлены в методической разработке " ИНФОРМАТИКА. Часть 2. Численные методы решения задач. Задания и методические указания к выполнению курсовой работы. Керчь 2003 ".
Варианты заданий определяются по последней цифре номера зачетной книжки.
З А Д А Н И Е 1. РЕШЕНИЕ ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ
ЗАДАЧА
Найти корни алгебраического уравнения F (x) =0 на промежутке[ хн,хк ]методом простых итераций. Предварительное отделение корней уравнения произвести путем табулирования функции F (x) на заданном промежутке с шагом, равным1/20от длины промежутка.
В качестве результата представить:
- преобразование исходного уравнения к виду x = СF (x)+ x с определением значения свободной константы С из условия сходимости метода;
- результат отделения корней;
- значение корня уравнения и количество итераций для его достижения для значений точности  =0.001, 0.0001, 0.00001.
=0.001, 0.0001, 0.00001.
ТАБЛИЦА ИНДИВИДУАЛЬНЫХ ВАРИАНТОВ
| № | Уравнение | Промежуток | № | Уравнение | Промежуток | |||
| х н | х к | х н | х к | |||||

| -3 | 
| ||||||

| -9,5 | 0,5 | 
| -10 | ||||

| -1,5 | 4,5 | 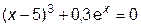
| -1 | ||||

| -1 | 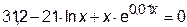
| ||||||

| -9 | -2 | 
|
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Какие уравнения называются трансцендентными?
2. Назовите два этапа решения трансцендентных уравнений в порядке их выполнения. В чем заключается идея первого этапа?
3. Запишите вывод формулы нахождения координаты точки Р в методе хорд. Запишите условие отбора отрезка, где находится искомый корень уравнения.
4. Почему в методе хорд нельзя использовать в качестве критерия окончания вычислительного процесса выполнение неравенства B-A< e?
5. Охарактеризуйте различие геометрической интерпретации метода Ньютона и модифицированного метода Ньютона. Какой из перечисленных методов имеет лучшую сходимость, а какой более прост в реализации?
6. Запишите итерационную формулу модифицированного метода Ньютона.
З А Д А Н И Е 2. АППРОКСИМАЦИЯ ЗАВИСИМОСТЕЙ.
ИНТЕРПОЛЯЦИОННЫЙ ПОЛИНОМ НЬЮТОНА
ЗАДАЧА
Даны узловые точки Х 1, Х 2, Х 3, Х 4, Х 5 и соответствующие им известные значения аппроксимируемой функции F (x): F 1, F 2, F 3, F 4, F 5.
Требуется:
1) построить интерполяционный полином Ньютона P 4(x) четвертого порядка.
2) построить график P 4(x) на промежутке [ X N, X K] с дискретностью 1/20 от длины промежутка;
В качестве результата представить:
- аналитическую запись полученного полинома;
- результаты вычисления полученного полинома в узловых точках Х 1, Х 2, Х 3, Х 4, Х 5
ТАБЛИЦА ИНДИВИДУАЛЬНЫХ ВАРИАНТОВ
| № | Узловые точки | Расчетные значения F (x) | [ X N, X K] | ||||||||
| X 1 | X 2 | X 3 | X 4 | X 5 | F 1 | F 2 | F 3 | F 4 | F 5 | ||
| -1,30 | 0,05 | 0,95 | 1,85 | 3,20 | 1,04 | 2,05 | 2,81 | 2,96 | 1,94 | [-4; 5] | |
| -0,70 | -0,10 | 0,70 | 1,50 | 1,90 | -0,36 | -0,05 | 0,36 | 0,93 | 1,40 | [-1,5; 2,5] | |
| 2,30 | 4,30 | 6,30 | 7,30 | 8,80 | 0,32 | -0,21 | 0,12 | 0,07 | [0,3; 10,3] | ||
| 2,20 | 2,80 | 3,40 | 3,70 | 4,15 | -1,34 | -1,09 | -1,27 | -1,54 | -2,67 | [1,6; 4,6] | |
| 2,10 | 4,10 | 5,70 | 7,30 | 8,10 | 1,89 | 1,74 | 1,53 | 1,36 | 1,29 | [1,3; 9,3] | |
| 1,80 | 2,70 | 3,60 | 4,50 | 6,30 | 0,37 | -0,24 | -0,67 | -0,59 | 0,51 | [1,2; 7,2] | |
| 2,50 | 4,00 | 6,50 | 7,50 | 9,00 | -0,34 | -0,09 | 0,27 | 0,43 | 0,70 | [1; 11] | |
| 1,15 | 1,30 | 1,50 | 1,75 | 1,85 | 2,28 | 4,09 | 5,13 | 4,78 | 6,02 | [1; 2] | |
| 5,20 | 7,20 | 8,40 | 10,00 | 11,20 | -6,97 | -5,61 | -6,69 | -11,08 | -13,16 | [4; 12] | |
| 4,10 | 4,30 | 4,70 | 4,90 | 5,10 | 0,81 | 1,12 | 0,53 | 0,1 | 0,04 | [3,5; 5,5] |
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что понимается под термином аппроксимация?
2. Сформулируйте условия Лагранжа при интерполяции.
3. Для аппроксимации функции F (x) на участке [ a, b ] был выбран интерполяционный полином Ньютона. После его построения были найдены значения функции в точке a < x 1< b и x 2> b. В каком случае ожидаемая точность полученного значения выше и почему?
4. Перечислите известные вам способы построения интерполяционного полинома.
5. В каком случае применение полинома Лагранжа более оправдано по сравнению с использованием канонического полинома и почему?
6. В чем состоит идея сплайн-интерполяции?
7. Почему в сплайн-интерполяции чаще всего применяют кубические сплайны?
8. Выберите правильный ответ на вопрос: "Что обеспечивается при интерполяции сплайнами?"
а) равенство значений производных;
б) равенство значений в узлах и непрерывность производных;
в) минимум максимального отклонения.
З А Д А Н И Е 3. АППРОКСИМАЦИЯ ЗАВИСИМОСТЕЙ.
МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
ЗАДАЧА
По имеющемуся набору экспериментальных данных о зависимости F (x) построить методом наименьших квадратов аппроксимирующие зависимости G (x) и H (x) в виде G (x)= A + Bx, H (x)= C e Dx и сравнить их по критерию «средний квадрат отклонения».
В качестве результата представить:
-аналитическую запись полученных функций G (x) и H (x);
-полученные для обеих функций значения среднего квадрата отклонения;
ТАБЛИЦА ИНДИВИДУАЛЬНЫХ ВАРИАНТОВ
| X | З н а ч е н и я ф у н к ц и и F(x) | X | З н а ч е н и я ф у н к ц и и F(x) | |||||||||
| Вар.0 | Вар.1 | Вар.2 | Вар.3 | Вар.4 | Вар.5 | Вар.6 | Вар.7 | Вар.3 | Вар.9 | |||
| 1,00 | 1,0763 | 1,2517 | 1,3230 | 0,6277 | 1,8814 | -1,00 | 1,2188 | 7,4220 | 0,8739 | 5,2215 | 0,7932 | |
| 1,00 | 1,0958 | 2,4367 | 1,4282 | 1,8690 | 1,8362 | -1,00 | 1,8744 | 7,2743 | 0,3451 | 5,2551 | 0,7023 | |
| 1,00 | 1,1383 | 1,1782 | 1,2831 | 0,4060 | 1,8883 | 0,10 | 2,5227 | 3,9034 | 0,2551 | 3,1721 | 0,6109 | |
| 1,40 | 1,0164 | 1,3449 | 1,1846 | 1,3298 | 1,4621 | 1,40 | 3,7513 | 1,9399 | 1,1792 | 1,8205 | 1,5195 | |
| 1,80 | 0,8448 | 0,8970 | 1,0423 | 2,2396 | 1,2024 | 1,80 | 3,2916 | 1,4080 | 2,7255 | 1,0110 | 1,1280 | |
| 1,80 | 0,8451 | 2,2131 | 0,9386 | 2,0336 | 1,1520 | 1,80 | 2,6521 | 1,4022 | 1,6945 | 1,4741 | 1,2064 | |
| 2,20 | 0,7522 | 1,3838 | 0,8643 | 1,4532 | 1,2381 | 1,90 | 3,7389 | 1,2177 | 1,7536 | 1,0859 | 2,0333 | |
| 2,20 | 0,7373 | 2,9157 | 0,8048 | 2,8410 | 1,0669 | 2,00 | 3,0509 | 1,2728 | 2,7337 | 1,1864 | 1,4756 | |
| 2,60 | 0,7308 | 3,0485 | 0,6675 | 2,3196 | 0,7721 | 2,00 | 3,7143 | 1,4258 | 2,1889 | 1,2272 | 1,9645 | |
| 3,00 | 0,6000 | 2,9941 | 0,5978 | 3,7697 | 0,5254 | 2,20 | 4,0200 | 1,3204 | 2,4792 | 1,0077 | 2,3354 | |
| 3,40 | 0,4993 | 6,2228 | 0,5266 | 3,4957 | 0,4590 | 2,40 | 3,7461 | 1,1501 | 2,5267 | 1,1415 | 3,0000 | |
| 3,40 | 0,5338 | 4,2152 | 0,5803 | 4,0342 | 0,5279 | 2,40 | 4,8381 | 1,0199 | 2,4428 | 1,1088 | 2,8193 | |
| 3,40 | 0,5165 | 6,6556 | 0,4813 | 3,7366 | 0,7434 | 3,00 | 5,0505 | 0,4076 | 4,3727 | 0,4204 | 2,9146 | |
| 3,80 | 0,4420 | 6,2930 | 0,5195 | 4,5619 | 0,6277 | 3,00 | 4,6304 | 0,4654 | 4,3626 | 0,7858 | 3,2616 | |
| 3,80 | 0,4321 | 6,6981 | 0,5007 | 5,2506 | 0,6442 | 3,30 | 5,9083 | 0,6565 | 4,7978 | 0,5386 | 3,3511 | |
| 4,20 | 0,3882 | 9,4535 | 0,4187 | 5,7408 | 0,5844 | 3,60 | 5,8075 | 0,3249 | 5,6142 | 0,6977 | 4,0366 | |
| 4,20 | 0,4114 | 8,2133 | 0,4140 | 5,3274 | 0,5569 | 3,60 | 5,8265 | 0,5175 | 5,6892 | 0,7369 | 3,7288 | |
| 4,20 | 0,4066 | 8,4742 | 0,4621 | 5,6536 | 0,1952 | 4,00 | 5,8601 | 0,1873 | 5,6279 | 0,1482 | 4,6823 | |
| 4,60 | 0,3975 | 11,9610 | 0,2657 | 7,4624 | 0,3174 | 4,00 | 7,3884 | 0,3377 | 5,3762 | 0,4855 | 5,5250 | |
| 5,00 | 0,3139 | 15,6451 | 0,1904 | 8,9393 | 0,3803 | 4,00 | 6,1544 | 0,2686 | 6,4613 | 0,2665 | 4,8807 |
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. В каких случаях целесообразно использовать для аппроксимации метод наименьших квадратов?
2. Что минимизируется в методе наименьших квадратов?
3. Зачем в методе наименьших квадратов величина e берется в квадрате?
4. От чего зависит выбор базисных функций в методе наименьших квадратов?
5. Какие базисные функции используются при линейной аппроксимации МНК?
6. Как получены формулы для коэффициентов C и D при экспоненциальной аппроксимации?
З А Д А Н И Е 4. ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
ЗАДАЧА
Требуется вычислить интеграл вида

где f (x) – подынтегральная функция, непрерывная на [ a,b ];
a,b – нижний и верхний пределы интегрирования.
Требуется вычислить значения интеграла SЛ, SП, Sс методами левых, правых и средних прямоугольников, и SТ1,SТ2 методом трапеций для двух разных разбиений n 1=10, n 2=20, по которым определить уточнение SР по Ричардсону.
В качестве результата представить:
1) значение интеграла SЛ, SП, Sс, вычисленные методами прямоугольников для n =20;
2) значения интеграла SТ1,SТ2, вычисленные методом трапеций для n 1=10, n 2=20;
3) уточнение по Ричардсону (SР);
5) ошибки значений SЛ, SП, Sс, SТ1, SТ2 по сравнению с SР.
ТАБЛИЦА ИНДИВИДУАЛЬНЫХ ВАРИАНТОВ
| № | Интеграл | [ a, b ] | № | Интеграл | [ a, b ] | |

| [0, 1.2] | 
| [-0.5, 1.0] | |||

| [-2, 2] | 
| [0, 4.5] | |||

| [0,3] | 
| [0, 10] | |||

| [-1, 1.4] | 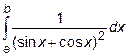
| [0, 2] | |||

| [-3, 3] | 
| [0.5, 3] |
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. В чем состоит суть методов численного интегрирования?
2. На что и как влияет количество разбиений при численном интегрировании? Можно ли увеличивая количество разбиений промежутка интегрирования бесконечно повышать точность интегрирования?
3. Как определяется значение частичного интеграла в методах прямоугольников?
4. Какой из методов прямоугольников имеет меньшую погрешность? Почему?
5. Выберите правильный ответ на вопрос: «Чем отличаются методы прямоугольников, трапеций, Симпсона?»
а) числом разбиений промежутка интегрирования;
б) поpядком аппроксимирующего полинома;
в) шагом интерполяции.
6. Учитывая формулы оценки погрешностей для метода средних прямоугольников и метода трапеций объяснить:
а) Почему величина S c получилась в 2 раза меньше, чем величина S Т2?
б) Почему величина S Т2 получилась в 4 раза меньше, чем величина S Т1?
З А Д А Н И Е 5. РЕШЕНИЕ ЗАДАЧИ КОШИ ДЛЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ПЕРВОГО ПОРЯДКА
ЗАДАЧА
Дано дифференциальное уравнение 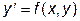 . Необходимо найти его решение методом Эйлера и методом Рунге-Кутта четвертого порядка при заданных начальных условиях y (x 0)= y 0 на заданном промежутке интегрирования [ x НАЧ, х КОН] с шагом, вычисленным по формуле: h =(x КОН- х НАЧ)/20.
. Необходимо найти его решение методом Эйлера и методом Рунге-Кутта четвертого порядка при заданных начальных условиях y (x 0)= y 0 на заданном промежутке интегрирования [ x НАЧ, х КОН] с шагом, вычисленным по формуле: h =(x КОН- х НАЧ)/20.
В качестве результата представить таблицу, содержащую следующие графы:
1) значения аргумента х;
2) решение, полученное методом Эйлера;
3) решение, полученное методом Рунге-Кутта 4-го порядка;
4) ошибка метода Эйлера по сравнению с методом Рунге-Кутта
и совместный график решений, полученных обоими методами.
ТАБЛИЦА ИНДИВИДУАЛЬНЫХ ВАРИАНТОВ
| № | Дифференциальное уравнение | Начальные условия | Пределы интегрирования | № | Дифференциальное уравнение | Начальные условия | Пределы интегрирования | |

| y(0)=0.35 | [0, 2] | 
| y(0)=e | [0, 1] | |||

| y(0)=0.15 | [0, 2] | 
| y(0)=1.0 | [0,  ] ]
| |||

| y(0)=1.35 | [0, 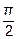 ] ]
| 
| y(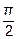 )=1 )=1
| [ 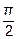 , , 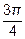 ] ]
| |||

| y(0)=2.18 | [0, 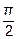 ] ]
| 
| y(1)=0 | [1, 2] | |||

| y(0)=0.34 | [0, 0.7] | 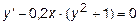
| y(0)=1.0 | [0, 2] |
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что является решением дифференциального уравнения?
2. Что является решением задачи Коши?
3. В чем заключается трудность численного решения задачи Коши с помощью рядов Тейлора?
4. Охарактеризуйте две группы методов решения задачи Коши.
5. Почему методы решения задачи Коши, использованные в данной работе, называются одношаговыми?
6. Каковы порядки точности использованных методов?
7. Какие источники погрешностей, связанные с численным решением задач Вы знаете?
8. Охарактеризуйте критерий для автоматического изменения шага интегрирования по методу Кутта-Мерсона.






