Одной из наиболее важных задач в условиях использования газотурбинного энергопривода на газопроводах является задача обеспечения наиболее экономичных режимов работы ГПА при перекачке заданного количества газа, что всегда связано с экономией топливного газа по станции.
Отклонение фактического режима от оптимального может быть обусловлено целым рядом причин, в частности снижением технического состояния агрегата как за счет нагнетателя, так и за счет снижения характеристик собственно ГТУ. В первом случае оценку снижения технического состояния из-за нагнетателя можно оценить по сдвигу характеристики собственно нагнетателя и, в частности, по изменению его политропного КПД в зависимости от производительности, hпол. = f (Q, n), а во втором - по сдвигу характеристики эффективного КПД ГТУ в зависимости от ее мощности, hе = f (Ne, Pнар., tнар.).
Изменение политропного КПД нагнетателя на примере установки типа ГТК-10 представлено на Рис. 5. 14., где обычная характеристика изменения приведенного КПД нагнетателя типа 370-18-1 развернута по частоте вращения его вала с использованием соотношения 5.2:
n = n0 
, (5.23)
где n0 и n - соответственно номинальная и текущая частота вращения силового вала; Qпр. – приведенная объемная производительность нагнетателя.
Изменение частоты вращения вала нагнетателя (Рис. 5.14) осуществляется до величины 3250 с интервалом между рассматриваемыми характеристиками 250 об./мин. и весьма наглядно показывает как изменяется относительный КПД нагнетателя при изменении подачи газа и частоты вращения его вала.
Естественно, что при рассмотрении характеристики нагнетателя в достаточно широком диапазоне изменения частоты вращения его вала, необходимо выдерживать условие работы нагнетателя в допустимой зоне работы, nmin £ n £ nmax. [16].
Рассмотрение данных Рис. 5.14 показывает, что значительный перерасход топливного газа на величину 3-6 % связан с характером зависимости hпол. = f (Qпр.), характеризующей резкое падение КПД нагнетателя по краям этой характеристики.
Для достижения максимального политропного КПД нагнетателя необходимо выдерживать оптимальные режимные значения e, Q и n, соответствующие hпол. = max, которые не всегда соответствуют оптимальным значениям по этой зависимости (Рис. 5. 14) и что связано с несогласованностью характеристик нагнетателя и газопровода.
Результаты эксплуатационных данных показывают, между изменением в расходе топливного газа по ГПА и политропгым КПД нагнетателя существует следующая простая зависимость [14]:
DВ = 1,1Dhпол. (5. 24)
Полученное соотношение показывает, насколько важно в условиях эксплуатации обеспечить условие работы нагнетателей на режимах hпол. = max. Уравнение (5.24) показывает, что снижение численного значения КПД нагнетателя только на 1% приводит к перерасходу топливного газа на 1,1%.
Выбор оптимальной частоты вращения вала нагнетателя, осуществляемый по условию hпол. = max. в практических условиях может быть проведен по предварительному определению диапазона изменения подачи газа по нагнетателю по его характеристике в зоне наивысшего значения КПД нагнетателя.
Соответственно может быть определено и соотношение давлений сжатия по первому нагнетателю (в условиях двухступенчатого сжатия) по условию hпол. = max. [16]:
(5.25)
Второй последовательно работающий в группе агрегат также должен работать при максимальном значении политропного КПД. Его объемная производительность в этом случае будет определяться соотношением:
Q2 = Q1 
(5.26)
Оптимальная частота вращения для этой производительности, а также соотношение давлений сжатия определяются по следующим соотношениям:
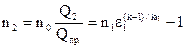(5.27)
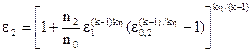(5.28)
где h - максимальное значение политропного КПД нагнетателя.
При использовании полнонапорных нагнетателей в качестве расчетного уравнения используется практически только уравнение (5.25).
С учетом приведенных соотношений, оптимальная зона работы нагнетателя типа 370-18-1 по условию максимального КПД ГТУ будет характеризоваться данными Рис. 5.15.
Значительный интерес всегда представляет совмещение характеристик нагнетателя и ГТУ с целью оценки совпадения значений их максимальных КПД. Решение этой задачи начинается прежде всего с определения мощности, потребляемой нагнетателем, при которой выполняется условие hпол. = max.
Определение мощности, потребляемой нагнетателем, можно осуществить с использованием известных формул приведения (для двухступенчатого сжатия):
(5.29)
(5.30)
где rвх.,i - плотность газа на входе в соответствующую группу нагнетателей.
При использовании полнонапорных нагнетателей расчетные соотношения несколько упрощаются и для определения мощности можно использовать только соотношение (5.29).
Переход к характеристикам газотурбинной установки осуществляется по условию равенства мощностей нагнетателя и ГТУ, Nе,ГТУ = Ni,наг. + Nмех., где Nмех. – механические потери мощности в системе соединения турбины и нагнетателя.
Зависимость эффективного КПД ГТУ от ее мощности определяется соотношением:
; 
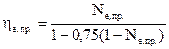(5.31)
Результаты совмещения характеристик нагнетателя и газовой турбины с учетом соотношений (5.2 и 5.25-5.31) приведены на Рис. 5.16.
Приведенная номограмма совмещения оптимальных режимов работы ГПА по условиям максимального значения КПД нагнетателя и ГТУ дает возможность при заданной производительности нагнетателя в первом приближении определять и оптимальную температуру газов перед турбиной высокого давления, при которой КПД также будет иметь максимальное значение.
Приведенная относительная мощность установки от приведенной температуры газов перед газовой турбиной в первом приближении определяется соотношением [6]:
Ne,пр. = 1 – 4,2 (1- Ттвд, пр.) Ттвд,пр. (5.32)
В условиях, когда температуру газов перед ТВД определить сложно, ее можно определить расчетным путем по известной температуре газов за ТНД.
Следует отметить, что аналогичным образом могут быть построены номограммы и для других типов ГПА с другими нагнетателями и другими типами газотурбинных установок.
Приведенная относительная температура газов за ТНД в зависимости от приведенной мощности установки в первом приближении может быть определена по соотношению:
Ттнд, пр. = 1 – 0,165 (1 – Nе,от. пр.) (5.33)
Наличие уравнений (5.32) и (5.33) позволяет легко построить графические зависимости между переменными, входящими в эти соотношения для различных режимов работы и по ним судить как изменяются эти одни из основных параметров ГТУ в процессе эксплуатации.
Задача 5.3. О пределить техническое состояние агрегата типа ГТК-10-4 с нагнетателем 370-18-1, а также его технические показатели (подачу нагнетателя, мощность ГПА, расход топливного газа, политропный КПД нагнетателя, а также эффективный КПД установки). Режим работы агрегата характеризуется следующими исходными данными: давление газа на входе в нагнетатель Р1 = 5,3 МПа, давление на выходе нагнетателя Р2 = 6,3 МПа, температура газа на входе нагнетателя t1 = 19,9 0C, температура газа на выходе нагнетателя t2 = 38,7 0C; частота вращения силового вала ГПА, n = 4650 об/мин. Температура газа на входе в ТВД t3 = 770 0C, температура воздуха на входе в осевой компрессор tвх.= 10 0С. Давление воздуха на входе в осевой компрессор Рвх. = 0,1 МПа Низшая теплота сгорания топливного газа Qнр = 33500 кДж/м3. Содержание метана в газе r = 0,97. Газовая постоянная R = 490 Дж/кгК. Коэффициент сжимаемости газа z = 0,94.
Решение. Решение данной задачи осуществляется в следующей последовательности: вначале оценивается техническое состояние нагнетателя, затем определяется потребляемая им мощность и подача газа. Найденная величина мощности используется как для определения технического состояния газотурбинной установки, так и для определения расхода топливного газа и эффективного КПД самой ГТУ.
Средние значения температуры и давления в процессе сжатия:
tm = (t1 + t2)/2 = (19,9 +38,7)/2 = 29,3 0C,
Pm = (P1 + P2)/2 =(5,3 + 6,8)/2 = 5,8 МПа.
Средняя изобарная теплоемкость любого природного газа в процессе сжатия может быть определена по следующему эмпирическому соотношению в зависимости от процентного содержания метана в газе и параметров процесса сжатия [ ], В данном примере ее можно принять равной Сpm = 2,17 кДж/кг0С.
Для определения реальной удельной работы сжатия газа в нагнетателе, его следует рассматривать как реальный газ, функции которого определяются в зависимости от двух переменных (например, P,t), с учетом коэффициента Джоля-Томпсона, характеризующим отличие реального газа от идеального.
В расчетное уравнение для определения удельной работы сжатия входит комплекс CpDh, который может быть подчитан по следующему уравнению [ ]:
(CpDh)m = (1,37-0,37rмет.)[(0,00012t22 -0,0135t2 +0,31)Pm-0,0463t2+11,19]=
