Пирсон предложил несколько методов с аппроксимацией обратного гессиана без явного вычисления вторых производных, т.е. путем наблюдений за изменениями направления антиградиента. При этом получаются сопряженные направления. Эти алгоритмы отличаются только деталями. Приведем те из них, которые получили наиболее широкое распространение в прикладных областях.
Алгоритм Пирсона № 2.
В этом алгоритме обратный гессиан аппроксимируется матрицей Hk, вычисляемой на каждом шаге по формуле
Hk+1= Hk+ 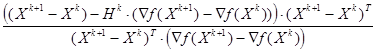 .
.
В качестве начальной матрицы H0выбирается произвольная положительно определенная симметрическая матрица.
Данный алгоритм Пирсона часто приводит к ситуациям, когда матрица Hkстановится плохо обусловленной, а именно - она начинает осцилировать, колеблясь между положительно определенной и не положительно определенной, при этом определитель матрицы близок к нулю. Для избежания этой ситуации необходимо через каждые n шагов перезадавать матрицу, приравнивая ее к H0.
Алгоритм Пирсона № 3.
В этом алгоритме матрица Hk+1определяется из формулы
Hk+1 = Hk + [Xk+1-Xk-Hk× (Ñf(Xk+1)-Ñ f(Xk))] ×
× 
Траектория спуска, порождаемая алгоритмом, аналогична поведению алгоритма Дэвидона-Флетчера-Пауэлла, но шаги немного короче. Пирсон также предложил разновидность этого алгоритма с циклическим перезаданием матрицы.
Проективный алгоритм Ньютона-Рафсона
Пирсон предложил идею алгоритма, в котором матрица рассчитывается из соотношения
Hk+1= Hk+  ,
,
H0=R0, где матрица R0такая же как и начальные матрицы в предыдущих алгоритмах.
Когда k кратно числу независимых переменных n, матрица Hkзаменяется на матрицу Rk+1, вычисляемую как сумма
Rk +  .
.
Величина Hk×(Ñf(Xk+1) - Ñf(Xk)) является проекцией вектора приращения градиента (Ñf(Xk+1)-Ñf(Xk)),ортогональной ко всем векторам приращения градиента на предыдущих шагах. После каждых n шагов Rk является аппроксимацией обратного гессиана H-1(Xk), так что в сущности осуществляется (приближенно) поиск Ньютона.






