Необходимость. Пусть функция 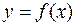 дифференцируема в точке х, т.е. её приращение в этой точке записывается в виде
дифференцируема в точке х, т.е. её приращение в этой точке записывается в виде  . Здесь А не зависит от
. Здесь А не зависит от 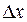 , а
, а  – бесконечно малая более высокого порядка по сравнению с
– бесконечно малая более высокого порядка по сравнению с 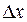 , т.е.
, т.е.  , где
, где 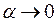 при
при 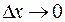 . Тогда
. Тогда 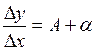 ,
,  . Следовательно, производная
. Следовательно, производная  существует и равна А.
существует и равна А.
Достаточность. Пусть функция 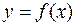 имеет производную в точке х, т.е.
имеет производную в точке х, т.е. 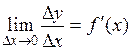 . Тогда имеем
. Тогда имеем  , где
, где 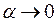 при
при 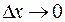 . Следовательно,
. Следовательно,  , т.е. функция
, т.е. функция 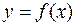 дифференцируема в точке х, что и требовалось доказать.
дифференцируема в точке х, что и требовалось доказать.
Замечания: 1). Из теоремы следует равносильность утверждений о дифференцируемости функций в точке и о существовании конечной производной функции в этой точке.
2). Коэффициент 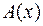 в разложении (1) равен производной функции
в разложении (1) равен производной функции 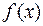 , т.е.
, т.е. 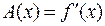 , что следует из доказательства необходимого условия теоремы. Таким образом,
, что следует из доказательства необходимого условия теоремы. Таким образом,
 . (2)
. (2)
3). Из определения дифференциала имеем
 , или
, или 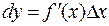 . (3)
. (3)
В частности, для 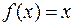 по формуле (3.15) получаем
по формуле (3.15) получаем 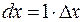 , и тогда
, и тогда
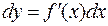 , или
, или 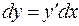 . (4)
. (4)
Из последней формулы следует, что производную функции можно рассматривать как отношение дифференциалов. Таким образом, имеем ещё одно обозначение производной функции  :
:
 , или
, или 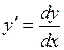 .
.
Пример: Найти в произвольной точке х дифференциал функций:
а)  б)
б) 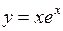 .
.
Решение: По формуле (4) получаем:
а) 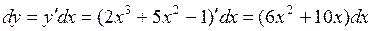 ;
;
б) 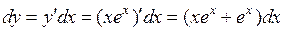 .
.
Необходимое условие дифференцируемости функций: если функция 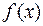 дифференцируема в точке
дифференцируема в точке  , то она имеет производную в этой точке.
, то она имеет производную в этой точке.
Свойства дифференциала:
1) 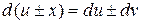 ; 2)
; 2)  ;
;
3)  ; 4)
; 4) 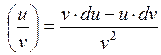 ,
, 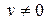 .
.
Пример: Найти 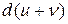 ,
, 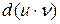 ,
, 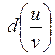 , если
, если 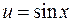 и
и 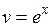 .
.
Решение:
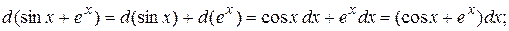
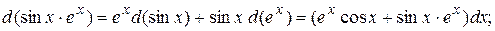


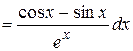 .
.




