Методические указания к проведению лекционного занятия
Тема № 3.6. Дифференциал функции.
План:
1. Дифференциал функции.
2. Геометрический смысл дифференциала.
3. Приближенные вычисления с помощью дифференциала.
4. Дифференциалы высших порядков.
Дифференциал функции
Функция 
называется дифференцируемой в точке 
, если приращение 
этой функции в точке , отвечающее приращению аргумента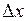 
, можно представить в виде
, (1)
где А – функция, зависящая только от и не зависящая от ,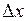 
– бесконечно малая более высокого порядка по сравнению с .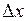
Замечание: Приращение аргумента может быть как положительным, так и отрицательным.
Опр.: Выражение 
в разложении (1) дифференцируемой в точке функции, являющееся главной линейной относительно 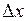частью приращения функции 
, называется дифференциалом функции в этой точке и обозначается
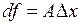или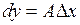 
.
При 
дифференциал функции по определению считается равным нулю.
Пример: Найти дифференциал функци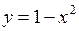и 
при 
.
Решение: Так как 
, то 
= 
Отсюда 
.
Окончательно находим
.
Опр.: Функция называется дифференцируемой на некотором интервале (а, b), если она дифференцируема в каждой точке этого интервала. Тогда в разложении (1) коэффициент А будет функцией х, а дифференциал 
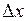будет функцией х и , т.е. 
.
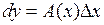Теорема. Для того чтобы функция была дифференцируема в точке х, необходимо и достаточно, чтобы в этой точке существовала производная 
.
