Решение. 1. Определение расчетных параметров поперечного сечения балки (рис

1. Определение расчетных параметров поперечного сечения балки (рис. 5.22, а). Ширина верхней полки b ₁ = = 0,7× h_CT = 0,7×0,34 = 0,238 м, принимаем b ₁ = 0,24 м; толщина верхней полки d₁ = 0,1× h_CT = 0,1×0,34 = 0,034 м; площадь сечения верхней полки м², ширина нижней полки b ₂ = 0,9× h_CT = 0,9×0,34 = 0,306 м, принимаем b ₂ = 0,3 м; тол­щина нижней полки d₂ = 0,07× h_CT = 0,07×0,34 = 0,0238 м, принима­ем d₂ = 0,024 м; площадь сечения нижней полки 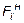= 0,3×0,024 = =0,0072 м², толщина стенки d = 0,4×d₁ = 0,4×0,034 = 0,0136 м, при­нимаем d = 0,014 м; площадь сечения стенки F_CT = 0,34×0,014 = = 0,00476 м²; высота балки h _d = h_CT + d₁ + d₂ = 0,34 + 0,034 + + 0,024 = 0,398 м.

Определение площади поперечного сечения балки.

м².

Определение центра тяжести поперечного сече­ния балки. Ось y является осью симметрии сечения балки, следо­вательно, центр его тяжести находится на этой оси. За вспомогатель­ную ось для определения координаты центра тяжести сечения на оси y принимаем ось x ₁ (рис. 5.22, а). Заметим, что поперечное сечение балки является составным, и включает в себя три прямоугольника (верхняя и нижняя полки, а также стенка). С учетом данного обстоятельства и воспользовавшись выражением (3.6), вычислим статический момент площади поперечного сечения балки относительно оси x ₁ :

Тогда положение центра тяжести на оси у определится ордина­той

м.

Определение момента инерции поперечного сечения балки относительно центральной оси (рис. 5.22). Значение момента инерции вычислим, пользуясь зависимостью между мо­ментами инерции относительно параллельных осей:

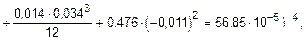
где , и - моменты инерции верхней и нижней полки и стенки, соответственно, относительно собственных горизонтальных осей, проходящих через их центры тяжести (см. п. 3.2),

2. Вычислить нормальные напряжения s по заданному изгибаю­щему моменту и построить их эпюру.

Момент сопротивления W_x для точек 1 и 2 определим по формулам:

для точки 1 м³;

для точки 2 м³,

где y ₁ = h _d - y _c = 0,398 - 0,205 = 0,193 м, y ₂ = y_C = 0,205 м.

Вычислим напряжения в точке 1 (рис. 5.22, а):

кН/м²» 53000 МПа < 167000 кН/м²

Вычислим напряжения в точке 2 (рис. 5.22, а):

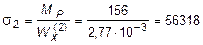кН/м²» 56000 МПа < 167000 кН/м²

Найдем значение нормальных напряжений в точке 3 по (5.10):

кН/м².

По полученным значениям s строим эпюру нормальных напря­жений (рис. 5.22, б).

Проверку прочности производим по формуле

,

где M_P - расчетный изгибающий момент; W_x - момент сопротивле­ния при изгибе; R_И - допускаемое напряжение при изгибе.

Допускаемое напряжение при изгибе равно:

кН/м².

Как видно, балка имеет значительное недонапряжение.

3. Определить значения касательных напряжений в точке 3.

Касательное напряжение определим по формуле Журавского:

,

где 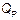- расчетная поперечная сила, d - ширина сечения на уровне точки 3.

Вычислим статический момент отсеченной части в точке 3 час­ти сечения :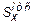

= 0,0072×(0,205 - 0,5×0,024)+

+ 0,00119×(0,096 + 0,125×0,34) = 1,544×10^-3 м³,

где = 0,25× h_CT ×d = 0,25×0,34×0,014 = 0,00119 м².

Вычислим касательное напряжение в точке 3:

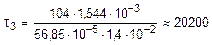кН/м².

 

 

4. Определить значения главных напряжений в т. 3 и указать их направления (показать главные площад­ки), имея в виду, что сечение относится к левой час­ти балки.

Главные напряжения в точке 3 определяем по формуле:

.

Подставив в данную формулу значения s₃ и t₃ , получим:

кН/м²;

кН/м².

В заключение найдем положение главных площадок и направ­ление главных напряжений (рис. 5.22, в).

При отрицательном угле a₀ откладываем его от нормали к сече­нию (площадке) по часовой стрелке и показываем положение глав­ных площадок и направление главных напряжений (рис. 5.22).