Теперь проведем второй эксперимент, со второй версией рассматриваемой программы. Предположим, что задан следующий вопрос:
?- 1! 7, Y).
Y - 4
Проанализируем, что при этом произошло. Была предпринята попытка проверить все три правила, и только после этого был получен ответ. Таким образом, выработана приведенная ниже последовательность целей.
• Попытка применить правило 1. Цель 7 < 3 не достигается; выполнить возврат и попытаться применить правило 2 (оператор отсечения не был применен).
• Попытка применить правило 2. Цель 3 =< 7 достигается, но затем не достигается цель 7 < 6; выполнить возврат и попытаться применить правило 3 (оператор отсечения не был применен).
• Попытка применить правило 3. Цель 6 =< 7 достигается.
Глава 5. Управление перебором с возвратами 123
Эта трассировка выполнения позволяет обнаружить еще один источник неэффективности. Вначале было установлено, что выражение X < 3 не является истинным (цель 7 < 3 не достижима). Следующей целью является 3 =< X (цель 3 =< 1 достижима). Но нам известно, что после неудачного завершения первой проверки вторая проверка обязательно будет успешной, поскольку она является отрицанием первой. Следовательно, вторая проверка является избыточной и соответствующая цель может быть опущена. Справедливым является также аналогичное утверждение в отношении цели 6 «< X в правиле 3. Эти рассуждения приводят к созданию приведенной ниже более лаконичной формулировки трех правил.
Если X < 3, то Y = О,
иначе, если *.'. •: 6, тс Y = Г., иначе Y = 4.
Теперь мы можем удалить из программы условия, которые гарантированно будут истинными при каждом их выполнении. Это позволяет получить третью версию данной программы:
f (X, 0):- X < 3,!. f (X, 2):- X < 6,!. flX, 4).
Эта программа вырабатывает такие же результаты, что и первоначальная версия, но является более эффективной по сравнению с обеими предыдущими версиями. Но что произойдет, если операторы отсечения будут удалены именно в этой версии? Программа примет следующий вид: fiх, 0):- х < з.
£(X, 2):- X < 6. f (X, 4).
Такая программа, в отличие от предыдущих, способна вырабатывать несколько решений, причем некоторые из них являются неправильными, как, например, при получении ответов на следующий вопрос:
?- f (1, YI.
У = 0;
У = 2;
Y = 4;
ПО
Важно отметить, что, в отличие от второй версии данной программы, на этот раз операторы отсечения не только влияют на процедурное поведение, ко и изменяют результаты программы.
Более точное значение механизма отсечения описано ниже.
Назовем родительской целью ту цель, которая согласована с головой предложения, содержащего оператор отсечения. Если в качестве цели обнаружен оператор отсечения, эта цель немедленно достигается, но приводит к фиксации в системе всех результатов выбора, полученных с того момента, как была вызвана родительская цель, и до того момента, как встретился оператор отсечения. Все оставшиеся альтернативы между родительской целью и оператором отсечения отбрасываются.
Чтобы пояснить это определение, рассмотрим некоторое предложение, заданное в следующей форме:
Н: - Б1, В2,..., Вт,!,..., Вп.
Предположим, что это предложение вызывается целью G, которая согласована с Н. В этом случае G представляет собой родительскую цель. Ко времени обнаружения оператора отсечения система уже нашла некоторое решение, соответствующее целям В1,.... Вг.. После выполнения оператора отсечения это (текущее) решение 51, -.., Вт замораживается и все возможные оставшиеся альтернативы отбрасываются. Кроме
124 Часть I. Язык Prolog
^
того, цель G теперь становится зафиксированной на данном предложении: все попытки согласовать цель G с головой какого-то другого предложения исключаются. Применим эти правила к следующему примеру:
!, 5, Т, V.
| С | :- Р, | Q, | R, |
| С | : - V. | ||
| А | :- В, | С, | D. |
? - к.
Здесь А, В, С, D, Р и т.д. имеют синтаксис термов. Оператор отсечения повлияет на выполнение цели С, как показано на рис. 5.3. Перебор с возвратами будет возможен в пределах списка целей?, Q, R, но как только будет достигнут оператор отсечения, все альтернативные решения в списке целей Р, Q, R подавляются. Альтернативное предложение, касающееся терма С, С:- v.
также отбрасывается. Но перебор с возвратами в пределах списка целей S, Т, и все еще возможен. Родительской целью в предложении, содержащем оператор отсечения, является цель С в следующем предложении:
А:- В, С, D.
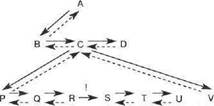
Рис. 5.3. Влияние оператора отсечения на выполнение программы. Начиная с терма А, сплошные стрелка обозначают последовательность вызовов, а пунктирные стрелки перебор с возвратами. Между термами R и S возможно только "одностороннее движение"
Поэтому оператор отсечения повлияет лишь на выполнение цели С. С другой стороны, он останется "невидимым" с позиций цели А. Таким образом, автоматический перебор с возвратами в пределах списка целей 3, С, D остается активным, несмотря на наличие оператора отсечения в предложении, используемом для достижения цели С.






