Третья программа решения задачи с восемью ферзями основана на следующих рассуждениях. Каждый ферзь должен находиться на некоторой клетке доски, т.е. в определенном вертикальном ряду, горизонтальном ряду, на восходящей и нисходящей диагонали. Для обеспечения того, чтобы все ферзи были в безопасности, их необходимо поместить на такие клетки, которые находятся в отличных от других вертикальных рядах, горизонтальных рядах, на разных восходящих и нисходящих диагоналях. Поэтому вполне естественно перейти к рассмотрению более развитого способа представления, с четырьмя координатами, как показано ниже.
Часть I. Язык Prolog
• х. Вертикальный ряд.
• у. Горизонтальный ряд.
• и. Восходящая диагональ.
• v. Нисходящая диагональ.
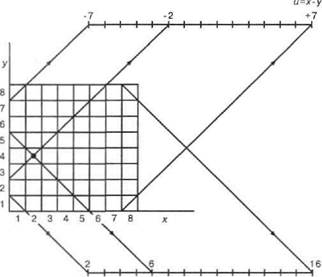
Эти координаты не являются независимыми: в частности, значения j и v зависят от значений х и у (как показано на рис. 4.7). Такую зависимость можно представить с помощью следующих уравнений: и = к - у
v = х + у
|
v=x+y
Рис. 4.7, Соотношение между координатами, заданными с помощью номеров вертикальных и горизонтальных рядов, а также восходящих и нисходящих диагоналей. Клетка, обозначенная точкой, имеет следующие координаты: х -
2, у = 4, и = 2 - 4 = -2.v = 2 + 4 - 6
Области определения для всех четырех измерений показаны ниже.
DX - [1,2,3,4,5,6,7,8]
Dy- [1,2,3,4,5,6,7,8]
Du = [-7,-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6,7]
Dv = [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16]
Теперь задачу с восемью ферзями можно сформулировать следующим образом: выбрать восемь четырехэлементных кортежей (X, Y, О. V) из соответствующих областей определения (X из Dx, V из Dy и т.д.), никогда не используя дважды одни и те же элементы из любой области определений. Безусловно, после выбора X и Y значения U и V становятся вполне определенными. Поэтому решение, грубо говоря, может состоять в следующем: учитывая все четыре области определения, выбрать позицию первого ферзя, удалить соответствующие элементы из этих четырех областей определения, а затем использовать остальную часть областей определения для размещения оставшихся ферзей. Программа, основанная на этой идее, приведена в листинге 4.4.
Глава 4. Использование структур: примеры программ
Позиция на доске снова представлена в виде списка координат Y. Основным отношением в этой программе является следующее отношение: sol mist, Dx, Су, Du, DV)
которое конкретизирует координаты Y ферзей (в списке Ylist) при условии, что эти ферзи помещены на подряд идущих вертикальных рядах, номера которых взяты из области определения Dx. Все координаты Y и все соответствующие координаты U и V берутся из списков Dy, Du и Dv. Процедура верхнего уровня, solution, может быть вызвана с помощью следующего вопроса:?- solution(S).
Ввод этого вопроса влечет за собой вызов отношения sol с полными областями определения, которые соответствуют пространству состояний задачи с восемью ферзями.
Листинг 4.4. Программа 3 для решения задачи с восемью ферзями
% solution; Ylist), если
% Ylist - список координат Y восьми ненападающих ферзей
solution(Ylist):-
sol(Ylist, % Координаты Y ферзей
[1,2,3,4,5,6,7,8], * Область определения координат X
[1,2,3,4,5,6,7,81, % Область определения координат Y
-7,-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6,7], * Восходящие диагонали [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16]). % Нисходящие диагонали
SOl ([], [], Dy, Du, Dv).
soli [Y I Ylist], [X | Dxl), Dy, Du, Dv):-
del(Y, Dy, Dyl), % Выбор координаты?
is.-;-Y, % Соответствующая восходящая диагональ
del( U, Du, Dull, % Удаление данных о ней
V is X+Y:. Соответствующая нисходящая диагональ
delf V, Dv, Dvl), % Удаление данных о ней
soil Ylist, Dxl, Dyl, Dul, Dvl). % Использование оставшихся значений
del[ Item, [ire- [ List], List).
delС Item, [First List], [First I Listl) ):-del(Item, List, Listl).
Процедура sol является универсальной в том смысле, что она может использоваться для решения задачи с N ферзями (на шахматной доске с размерами ЫхН), ДЛЯ этого достаточно только правильно задать области определения Dx, Dy и т.д.
Целесообразно механизировать выработку значений этих областей определения. Для этого требуется процедура gen(N1, N2, List)
которая после получения двух заданных целых чисел, N1 и N2, вырабатывает следующий список:
List = [ N1, N1 + 1, N1 + 2,..., N2 - 1, N2j
Такая процедура приведена ниже.
gen (И, N, [N]).
gen(N1, N2,:.: List]}:-
N1 < N2, Mis N1 + 1,
gent К, N2, List).
Отношение верхнего уровня, solution, необходимо обобщить соответствующим образом, определив его в форме: solution (N, S)
Часть I. Язык Prolog
где N — размер доски и S — решение, представленное в виде списка координат Y для N ферзей. Обобщенное отношение solution выглядит следующим образом:
solution(N, S):-
gen(1, В, Dxy), % Dxy - область определения для X и Y Nul is 1 - N, Bu2 is H - 1,
gen{Nul, Nu2f Du),
Mv2 is К + H,
gen; 2, Hv2, Dv},
soli 5, Dxy, Dxy, Du, Dv).
Например, решение задачи с 12 ферзями может быть получено с помощью следующего вопроса:?- solution* 12, S). 3 - [1,3,5,8,10, 12, б, 11, 2,7, 9, 45






