Рассмотрим принципиальные отличия неравновесных процессов от равновесных на примере расширения газа в цилиндре под поршнем, получающего теплоту 
от источника с температурой T1 и совершающего работу против внешней силы Р, действующей на поршень.
Расширение будет равновесным только в случае, если температура газа Т равна температуре источника (Т=Т1), внешняя сила Р равна давлению газа на поршень (P=pF) и при расширении газа нет ни внешнего, ни внутреннего трения. Работа расширения газа в этом случае равна 
, а изменение энтропии рабочего тела в таком процессе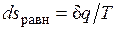 
.
Невыполнение хотя бы одного из указанных условий делает расширение газа неравновесным. Если неравновесность вызвана трением поршня о стенки цилиндра, то работа 
, совершаемая против внешней силы Р, оказывается меньше, чем pdv, так как часть ее затрачивается на преодоление трения и переходит в теплоту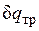 
. Она воспринимается газом вместе с подведенной теплотой q, в результате чего возрастание энтропии газа в неравновесном процессе 
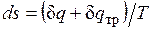оказывается больше, чем в равновесном при том же количестве подведенной от источника теплоты .
|
Рисунок 4.6 - К определению изменения энтропии в неравновесных процессах
Если неравновесность вызвана отсутствием механического равновесия (P<pF), поршень будет двигаться ускоренно. Быстрое движение поршня вызывает появление вихрей в газе, затухающих под действием внутреннего трения, в результате чего часть работы расширения опять превращается в теплоту 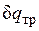. Работа против внешней силы снова получается меньше, а возрастание энтропии — больше, чем в равновесном процессе с тем же количеством теплоты .
Если неравновесность вызвана теплообменом при конечной разности температур (температура газа Т меньше температуры источника T1), то возрастание энтропии рабочего тела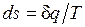 
оказывается больше, чем 
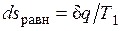в равновесном процессе из-за снижения температуры газа. При том же положении поршня, т. е. заданном удельном объеме v, меньшей температуре газа соответствует меньшее его давление р. Соответственно меньше должна быть и уравновешивающая сила Р': Р'=p'F<P=pF. Работа расширения против этой силы 
.
Итак, неравновесность всегда приводит к увеличению энтропии рабочего тела при том же количестве подведенной теплоты и к потере части работы. В общем виде это можно записать следующим образом:
; 
,
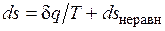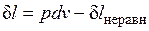Причем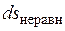 
и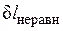 
всегда положительны.
Ранее было показано, что для равновесных процессов справедливо соотношение 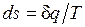. Разобранный пример достаточно наглядно показывает, что в неравновесных процессах 
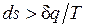, если — количество подведенной к системе или отведенной от нее теплоты, а T — температура источника теплоты. Обе записи являются аналитическими выражениями второго закона термодинамики:
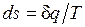— в равновесных процессах;
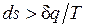— в неравновесных процессах.
Для изолированных систем, которые по определению не обмениваются теплотой с окружающей средой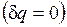 
, эти выражения приобретают вид
.
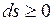Если в адиабатно-изолированной системе осуществляются равновесные процессы, то энтропия системы остается постоянной.
Самопроизвольные (а значит, и неравновесные) процессы в изолированной системе всегда приводят к увеличению энтропии. Это положение представляет собой наиболее общую формулировку второго начала термодинамики для неравновесных процессов, известную под названием принципа возрастания энтропии.
Следует подчеркнуть, что последнее неравенство применимо только к изолированным системам. Если от системы отводится теплота, то ее энтропия может убывать, однако суммарное изменение энтропии системы и энтропии внешних тел всегда положительно (либо равно нулю, если в системе протекают равновесные процессы).
Когда изолированная система находится в состоянии с максимальной энтропией, то в ней не могут протекать никакие самопроизвольные процессы, потому что любой самопроизвольный процесс неравновесен и сопровождается увеличением энтропии. Поэтому состояние изолированной системы с максимальной энтропией является состоянием ее устойчивого равновесия, и самопроизвольные процессы могут протекать в изолированной системе лишь до тех пор, пока она не достигнет состояния равновесия.
