The Laplace transform pairwas given in the Lecture 1.4; it is written as
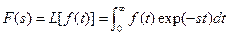(6.8)
And
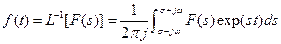(6.9)
where the complex variable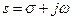 
. Similarly, the Fourier transform pairis written as
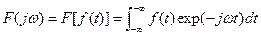(6.10)
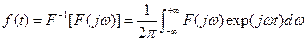(6.11)
The Fourier transform exists for f(t) when
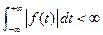(6.12)
The Fourier and Laplace transforms are closely related, as we can see by examining Equations (6.8) and (6.10). When the function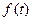 
is defined only for 
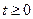, as is often the case, the lower limits on the integrals are the same. Then we note that the two equations differ only in the complex variable. Thus, if the Laplace transform of a function 
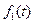is known to be 
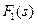, we can obtain the Fourier transform of this same time function by setting 
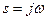in .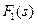
Again we might ask, since the Fourier and Laplace transforms are so closely related, why can't we always use the Laplace transform? Why use the Fourier transform at all? The Laplace transform permits us to investigate the s-plane location of the poles and zeros of a transfer function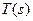 
. However, the frequency response method allows us to consider the transfer function 
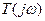and to concern ourselves with the amplitude and phase characteristics of the system. This ability to investigate and represent the character of a system by amplitude, phase
equations, and curves is an advantage for the analysis and design of control systems.
If we consider the frequency response of the closed-loop system, we might have an input r(t) that has a Fourier transform in the frequency domain as follows:
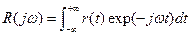(6.13)
Then the output frequency response of a single-loop control system can be obtained by substituting 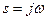in the closed-loop system relationship, Y(s) = T(s)R(s), so that we have
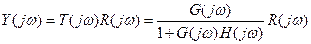(6.14)
Using the inverse Fourier transform, the output transient response would be
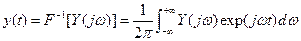(6.15)
However, it is usually quite difficult to evaluate this inverse transform integral for
all but the simplest systems, and a graphical integration may be used. Alternatively,
as we will note in succeeding sections, several measures of the transient response
can be related to the frequency characteristics and utilized for design purposes.
26
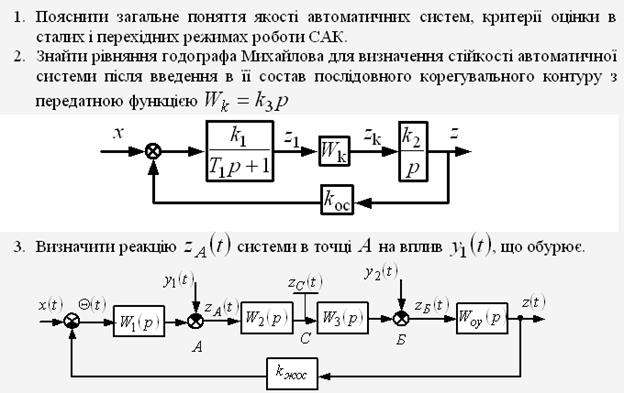
26.3 Define the value of M(t) signal after Z1(t) disturbance input signal is applied.
|
|
|
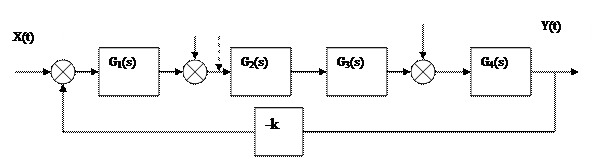
27
27.1 Explain the notion of control systems stability: determination of control systems stability using their step response characteristics.
