Приложение. Руководство пользователя WINPHI (CD-ROM):

основные принципы фибоначчи

"Дайте волю своему воображению". С этой фразы, с этого пригла­шения начиналась наша первая книга "Приложения и стратегии Фибоначчи для трейдеров". И вновь мы, не колеблясь, представля­ем читателям очарование открытия Леонардо Пизанского, более известного как Фибоначчи, публикуя этот призыв к творческому потенциалу и воображению.

Прошло восемь лет после издания книги "Приложения и стра­тегии Фибоначчи для трейдеров". Рыночная среда очень сильно из­менилась. Красоты природы, однако, остались неизменными. За­думайтесь обо всех чудесах природы в нашем мире: океанах, де­ревьях, цветах, растениях, животных и микроорганизмах.

Подумайте о достижениях людей в естествознании, ядерной теории, медицине, компьютерной технологии, радио и телевиде­нии. Наконец, подумайте о движениях тренда на мировых рын­ках. Вас может удивить, что все они имеют общий базовый стерео­тип: ряды суммирования Фибоначчи.

В первой главе описаны ряды суммирования Фибоначчи — ос­нова нашего рыночного анализа, ориентированного на фигуры графиков. После разъяснения значения этой последовательности чисел бросим быстрый взгляд на типы явлений и достижений в человеческом поведении, которые можно проанализировать с ис­пользованием рядов суммирования Фибоначчи. Затем мы приве­дем выводы инженера и трейдера Ральфа Нельсона Эллиота. Мы рассмотрим сделанные им обобщения, дающие сегодня аналити­кам неограниченную основу, которая может использоваться для прибыльной торговли на глобальных рынках.

Глава 1 написана как резюме книги "Приложения и стратегии Фибоначчи для трейдеров". Читатели, хорошо знакомые с теорией Фибоначчи и Эллиота, описываемой в данной главе, могут сразу перейти к краткому обзору нового материала в этой книге на стра­нице 39.

РЯДЫ СУММИРОВАНИЯ ФИБОНАЧЧИ

Фибоначчи (1170—1240) жил и работал торговцем и математиком в итальянском городе Пизе. Он один из самых прославленных ев­ропейских ученых своего времени. Среди его величайших дости­жений — введение арабских цифр, заменивших римские. Он раз­работал ряд суммирования Фибоначчи, который выглядит как

1-1-2-3-5-8-13-21-34-55-89-144-... или в математических выражениях

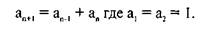
Математический ряд асимптотически (то есть приближаясь все медленнее и медленнее) стремится к постоянному отношению.

Однако это отношение иррационально; оно имеет бесконеч­ную, непредсказуемую последовательность десятичных значений, выстраивающихся после него. Оно никогда не может быть выра­жено точно. Если каждое число, являющееся частью ряда, разде­лить на предшествующее значение (например, 13-^8 или 21 -ИЗ), результат действия выразится в отношении, которое колеблется вокруг иррационального числа 1,61803398875..., чуть больше или чуть меньше соседних отношений ряда. Отношение никогда, до бесконечности, не будет точным до последней цифры (даже при использовании самых мощных компьютеров, созданных в наше время). Ради краткости, будем использовать в качестве отношения Фибоначчи число 1,618 и просим читателей не забывать об этой погрешности.

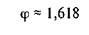
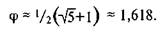
Это отношение стало обрастать разными особыми именами еще даже до того, как другой средневековый математик Лука Па-чиоли (1445—1514) назвал его "божественной пропорцией". Сре­ди его современных названий — "золотое сечение" и " золотая середина". Немецкий астроном Иоганн Кеплер (1571 — 1630) на­звал отношение Фибоначчи одним из сокровищ геометрии. В ал­гебре оно, как правило, обозначается греческой буквой ФИ (ср), а именно

или в иной математической форме

Но интерес ученых (и трейдеров, как мы увидим) привлекает не только ФИ. Если мы разделим любое число ряда суммирования Фибоначчи на число, следующее за ним в этом ряду (например, 8-^13 или 13-^21), мы найдем, что ряд асимптотически прибли­жается к отношению ФИ'

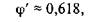
что является просто обратным значением ФИ, где

или в другой форме

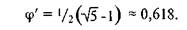
Это очень необычное и замечательное явление — и полезное, когда дело доходит до разработки инструментов торговли, как мы узнаем в ходе анализа. Поскольку первоначальное отношение ФИ иррационально, обратное значение ФИ' к отношению ФИ также обязательно иррациональное число. Это означает, что мы снова должны принимать во внимание небольшую погрешность при ис­пользовании для вычислений приближенного сокращенного зна­чения 0, 6 18.

А теперь аналитически используем ФИ и ФИ' и сделаем следу­ющий шаг, слегка переформулировав ряд суммирования Фибо­наччи так, чтобы в результате получился следующий ряд ФИ:

0,618-1,000-1,618-2,618-4,236-6,854-11, 090-17,944-... На математическом языке это записывается так:

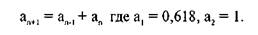
В данном случае мы не находим в этом отношении асимпто­тического процесса, потому что деление каждого числа ряда ФИ на его предшествующее значение (например, 4,236-^2,618 или 6,854-Н,236) дает приближенное отношение ФИ = 1,618. Вы­полнение деления в обратном направлении — а именно деление каждого числа ряда ФИ на следующее значение (например, 2,618^4,236 или 4,236-^6,854) — дает обратное значение кон­станты ФИ, названной нами ранее ФИ' = 0,618. Прежде чем двигаться далее по тексту, важно, чтобы читатели до конца по­няли, как получен ряд ФИ из основного ряда суммирования Фибоначчи.

Мы открыли для себя ряд простых чисел, введенных в науку Фибоначчи. Теперь сделаем еще одно краткое отступление преж­де, чем использовать ряд суммирования Фибоначчи как основу для разработки торговых инструментов. Сначала рассмотрим, ка­кое отношение имеет ряд суммирования Фибоначчи для окружа­ющей нас природы. После этого останется сделать лишь малень­кий шаг к выводам, прямо приведущих нас к уместности прило­жения ряда суммирования Фибоначчи к движению любых между­народных рынков: валютных или фьючерсных, фондовых или производных.

Мы учитываем уменьшенность колебаний частных вокруг зна­чения 1,618 (или 0,618 соответственно) в ряду Фибоначчи с помо­щью более высоких или низких чисел в волновом принципе Элли­ота, названном Ральфом Нельсоном Эллиотом правилом чередо­вания. И мы представляем инструменты торговли, разработанные нами для самого полного использования магии ФИ. Люди подсоз­нательно ищут божественную пропорцию. Это лишь постоянная и бесконечная борьба за создание более высокого уровня жизни.

ОТНОШЕНИЯ ФИБОНАЧЧИ

Мы — надеемся, и наши читатели — не перестаем удивляться, сколько постоянных значений можно рассчитать с использовани­ем последовательности Фибоначчи, и тому, как отдельные числа, формирующие последовательность, повторяются в столь многих вариациях. Однако ни в коем случае нельзя забывать, это не про­сто игра чисел; это самое важное из когда-либо открытых матема­тических представлений природных явлений. Следующие иллю­страции продемонстрируют некоторые интересные приложения этой математической последовательности.

Мы подразделили наши наблюдения на два раздела. Сначала кратко пройдемся по отношению Фибоначчи и его присутствию в природных явлениях и архитектуре. Затем кратко опишем, как ис­пользуют отношение Фибоначчи в математике, физике и астроно­мии.