¬ивчити в≥льн≥ затухаюч≥ коливанн€ пружинного ма€тника, визначити параметри коливальноњ системи та характеристики коливань (жорстк≥сть пружини, коеф≥ц≥Їнт опору, пер≥од коливань, логарифм≥чний декремент, коеф≥ц≥Їнт затуханн€), а також досл≥дити њх залежн≥сть в≥д маси ма€тника.
2. “еоретичн≥ в≥домост≥.
ѕружинним ма€тником називають систему, €ка складаЇтьс€ з невеликого т≥ла масою m, п≥дв≥шеного на вертикальн≥й пружин≥ жорстк≥стю k, другий к≥нець €коњ закр≥плений. ћасою пружини нехтують (рис. 1).
¬ положенн≥ р≥вноваги (x =0) сила т€ж≥нн€, що д≥Ї на кульку вр≥вноважуЇтьс€ силою пружност≥:
 , (1)
, (1)
де  - видовженн€ пружини в стан≥ р≥вноваги.
- видовженн€ пружини в стан≥ р≥вноваги.
 |
–ис. 1.
ѕри зм≥щенн≥ т≥ла в≥д положенн€ р≥вноваги сила пружност≥ буде б≥льшою або меншою за силу т€ж≥нн€ ≥ њхн€ р≥внод≥йна F буде направлена до положенн€ р≥вноваги, а њњ модуль дор≥внюватиме:
 (2)
(2)
«а законом √ука:
 , (3)
, (3)
де x Ц зм≥щенн€ системи в≥д положенн€ р≥вноваги,  - величина деформац≥њ пружини, знак У-Ф св≥дчить про те, що сила пружност≥ за напр€мком протилежна до деформац≥њ.
- величина деформац≥њ пружини, знак У-Ф св≥дчить про те, що сила пружност≥ за напр€мком протилежна до деформац≥њ.
ѕ≥дставимо у формулу (2) вирази (3) та (1) ≥ отримаЇмо:
 (4)
(4)
–≥внод≥йна сил пружност≥ ≥ т€ж≥нн€ пропорц≥йна зм≥щенню x ≥ направлена до положенн€ р≥вноваги, тобто Ї повертаючою силою, п≥д д≥Їю €коњ в систем≥ в≥дбуваютьс€ в≥льн≥ коливанн€.
р≥м повертаючоњ сили F на систему д≥Ї сила опору середовища, в €кому вона перебуваЇ.
 , (5)
, (5)
де r Ц коеф≥ц≥Їнт опору,  Ц швидк≥сть системи. «нак У-Ф св≥дчить про те, що сила опору направлена проти швидкост≥.
Ц швидк≥сть системи. «нак У-Ф св≥дчить про те, що сила опору направлена проти швидкост≥.
«апишемо закон динам≥ки дл€ руху т≥ла:
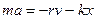 (6)
(6)
ѕ≥дставимо в це р≥вн€нн€ вираз дл€ швидкост≥ та прискоренн€ та отримаЇмо:

ѕод≥лимо р≥вн€нн€ на m ≥ введемо позначенн€:
 (7)
(7)
 , (8)
, (8)
де r, m, k Ц параметри пружинного ма€тника.
“од≥ остаточно диференц≥альне р≥вн€нн€ затухаючих коливань матиме вигл€д:
 . (9)
. (9)
–озвТ€зком цього р≥вн€нн€ Ї функц≥€:
 . (10)
. (10)
¬≥льн≥ коливанн€ пружинного ма€тника Ї затухаючими з ампл≥тудою  ,та частотою
,та частотою 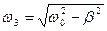 ; де
; де  - власна частота коливань пружинного ма€тника.
- власна частота коливань пружинного ма€тника.
«а формулою звТ€зку м≥ж пер≥одом та частотою отримаЇмо вираз дл€ пер≥оду коливань пружинного ма€тника:
 . (11)
. (11)
Ћогарифм≥чний декремент затуханн€, €кий характеризуЇ зменшенн€ ампл≥туди за пер≥од коливань, дор≥внюЇ:
 . (12)
. (12)
« р≥вн€нь (7), (11), (12) видно, що коеф≥ц≥Їнт затуханн€, пер≥од, логарифм≥чний декремент затуханн€ залежать в≥д параметр≥в системи.
3. ћетодика вим≥рюванн€.
ћетодика виконанн€ даноњ роботи пол€гаЇ в тому, що за вим≥р€ним значенн€м ампл≥туди коливань ј0 в початковий момент часу та ампл≥туди ј n через час t, за €кий в≥дбулось n коливань, визначаЇтьс€ пер≥од коливань T, коеф≥ц≥Їнт затуханн€ β та логарифм≥чний декремент затуханн€ δ за формулами:
 , (13)
, (13)
 , (14)
, (14)
|
|
|
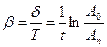 , (15)
, (15)
ƒл€ визначенн€ жорсткост≥ пружини використовуЇтьс€ додатковий т€гарець масою ћ, €кий додаЇтьс€ до т≥ла, п≥дв≥шеного на пружин≥, ≥ призводить до њњ додаткового видовженн€  .
.
“од≥ за умови р≥вноваги:

розкриЇмо дужки ≥ отримаЇмо:
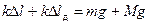 .
.
¬раховуючи вираз (1) остаточно отримаЇмо формулу дл€ розрахунку жорсткост≥ пружини:
 . (16)
. (16)
оеф≥ц≥Їнт опору r зг≥дно виразу (7):
 . (17)
. (17)






