8.5.1 Расчеты несущих конструкций локомотивов на циклическую долговечность выполняют:
- для оценки ожидаемого ресурса при проектировании;
- для оценки возможности продления назначенного срока службы (расчет остаточного ресурса);
- при изменении нагруженности.
8.5.2 Расчет долговечности (ресурса) проводят на основе гипотезы линейного суммирования повреждений.
Необходимыми исходными данными для расчета долговечности являются:
- результаты исследования напряженно-деформированного состояния детали, полученные расчетным либо экспериментальным путем;
- блок эксплуатационных нагрузок (например, в течение 1 года работы, 1 км пробега), полученный по результатам математического моделирования либо по результатам динамико-прочностных испытаний опытного образца локомотива и представленный в виде ступенчатой функции распределения амплитуд динамических напряжений, заданной парой чисел (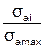
, ti), где 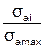– амплитуда напряжений i -го уровня, отнесенная к максимальному напряжению блока; ti – доля напряжений i -го уровня в общем блоке;
- параметры кривой усталости (предел выносливости σ–1∂, точка перелома N G и показатели степени наклона прямых, аппроксимирующих кривую усталости m 1 и m 2).
8.5.3 Если кривая усталости аппроксимирована наклонной и горизонтальной прямыми линиями, т. е. m 2 = 0, то напряжения менее 0,5σ–1∂ в расчете не учитывают и используют уравнение
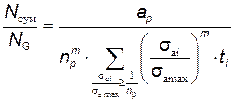, (8.21)
где N сум – суммарное количество циклов за срок службы детали;
N G – число циклов, соответствующее точке перелома кривой усталости;
a p – параметр, корректирующий линейную гипотезу накопления повреждений при нерегулярном нагружении, для локомотивных конструкций принимают равным 0,5 – 1,0;
n p – коэффициент перегрузки.
П р и м е ч а н и я:
1 Согласно корректированной линейной гипотезе накопления повреждений условие разрушения имеет вид
.
2 Коэффициент перегрузки определяется соотношением
,
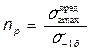где 
– максимальное напряжение в предельном блоке нагружения, который подобен действующему и вызывает разрушение при числе циклов N сум.
Уравнение (8.21) позволяет определить медианное (соответствующее вероятности разрушения 50 %) число циклов.
8.5.4 Для расчета долговечности, соответствующей вероятности разрушения p, используют формулу
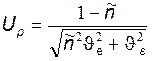, (8.22)
где U p – квантиль нормального распределения, соответствующая вероятности разрушения p, %;
– относительный коэффициент запаса;
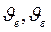– коэффициенты вариации нормально распределенных величин предела выносливости σ –1∂ и максимального напряжения σ amax в действующем блоке нагружения.
Коэффициенты вариации при расчете принимают равными 0,10 – 0,15.
Относительный коэффициент запаса вычисляют по формуле
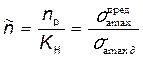, (8.23)
где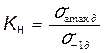 
– действительный коэффициент нагруженности детали.
8.5.5 Для кривой усталости, аппроксимируемой двумя наклонными прямыми линиями с показателями наклона m 1 и m 2, используют уравнение, аналогичное уравнению (8.21):
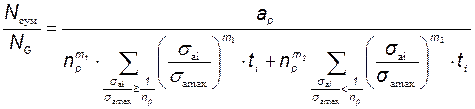(8.24)
В этом случае при расчете учитывают все напряжения из блока нагружения.
8.5.6 Порядок расчета:
- по уравнениям (8.21) или (8.24) строят кривую зависимости суммарного числа циклов 
от коэффициента перегрузки n p;
- по этой кривой для заданного срока службы, выраженного суммарным числом циклов N сум, определяют соответствующее значение n p;
- вычисляют значения действительного коэффициента нагруженности K Н и относительного коэффициента запаса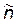 
по (8.23);
- по формуле (8.22) вычисляют значения квантилей U p, и по таблице нормального закона распределения определяют вероятность разрушения p или безотказной работы (1 – p).
8.5.7 Рассчитанная вероятность разрушения базовой части p в течение назначенного срока службы должна быть не более 10-4 (0,01 %).
8.5.8 Расчет может быть выполнен в обратном порядке, т. е., задавшись вероятностью разрушения детали p = 0,0001, по уравнениям (8.21) или (8.24), формулам (8.22) и (8.23) определяют долговечность N сум, соответствующую этой вероятности.
Пример расчета долговечности приведен в приложении В.
