ТРАНСПОРТНА ЗАДАЧА ЛIНIЙНОГО ПРОГРАМУВАННЯ
Змiстовна постановка та формальна модель транспортної задачi лiнiйного програмування
Нехай є m пунктів виробництва однорiдної або взаємозамінної продукції. Кожний з пунктів виробництва позначимо через  , де i= 1, …, m. Через
, де i= 1, …, m. Через 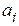 будемо позначати обсяг продукції, що виробляють у пункті
будемо позначати обсяг продукції, що виробляють у пункті  . Нехай є n пунктів споживання (призначення) цієї продукції, кожний з яких позначимо через
. Нехай є n пунктів споживання (призначення) цієї продукції, кожний з яких позначимо через  , де j=1,..., n, а обсяг споживання (попиту) продукції в пункті
, де j=1,..., n, а обсяг споживання (попиту) продукції в пункті  – через
– через  . Вартість перевезення одиниці продукції від i-го виробника j-го споживача складає
. Вартість перевезення одиниці продукції від i-го виробника j-го споживача складає  (i=1,..., m, j=1, …, n). Припускається, що транспортні витрати на перевезення між будь-якою парою пунктів пропорційні обсягу продукту, який перевозять.
(i=1,..., m, j=1, …, n). Припускається, що транспортні витрати на перевезення між будь-якою парою пунктів пропорційні обсягу продукту, який перевозять.
Потрібно встановити такі обсяги перевезень  від кожного виробника до кожного споживача, щоб сумарні витрати на перевезення були мінімальними, а потреби всіх споживачів – задоволені (якщо тільки обсяг можливих поставок покриває загальний обсяг споживання).
від кожного виробника до кожного споживача, щоб сумарні витрати на перевезення були мінімальними, а потреби всіх споживачів – задоволені (якщо тільки обсяг можливих поставок покриває загальний обсяг споживання).
Математична модель задачі така:
 (5.1)
(5.1)
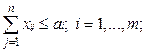 (5.2)
(5.2)
 (5.3)
(5.3)
 (5.4)
(5.4)
У (5.1)  являє собою сумарні транспортні витрати.
являє собою сумарні транспортні витрати.
Задача (5.1) – (5.4) є ЗЛП і називається транспортною задачею лінійного програмування (ТЗЛП). Така назва пов’язана зі структурою задачі, а не зі змістовною постановкою. До моделі вигляду (5.1) – (5.4) може привести задача, за своїм змістом ніяк не пов’язана з транспортом та плануванням перевезень. У такому разі кажуть, що задачу можна сформулювати в термінах транспортної задачі.






