ü Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты. S =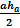 
ü Формула площади треугольника по трем сторонам. Формула Герона
S =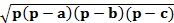 
p = 
ü Формула площади треугольника по двум сторонам и углу между ними/
Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.
S = 
abSinɤ
ü Формула площади треугольника по трем сторонам и радиусу описанной окружности
S = 
ü Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.
S = pr
ü Следствие 1. Площадь прямоугольного треугольника равна половине произведения катетов.
ü Следствие 2. Если высоты двух треугольников равны, то их площади относятся как основания.
ü Теорема. Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы.
= 
Теорема Пифагора
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
a2 + b2 = c2
Подобные треугольники
Подобные треугольники — треугольники, у которых углы соответственно равны, а стороны одного пропорциональны сходственным сторонам другого треугольника.
Теорема. Отношение площадей
двух подобных треугольников
равно квадрату
коэффициенту подобия.
