Пример 1. Найти интервалы возрастания и убывания функции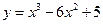 
.
Решение: Функция определена на всей числовой прямой, т.е.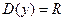 
.
1. Найдём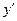 
.
.
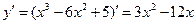2. Найдём критические точки.
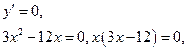
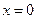или 
.
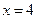3. Заполним таблицу:
| 
| 
| 
| ||
|
| + | - | + | ||
| 
| 
| 
|
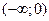
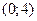
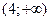
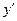
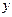
Таким образом, функция 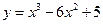возрастает на интервалах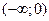 
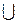
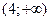, а убывает на интервале .
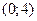Пример 2. Найти экстремумы функции .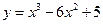
Решение: Функция определенна на всей числовой прямой, т.е. .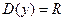
1.Найдём .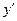
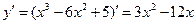
2.Найдём критические точки.
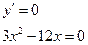
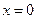или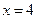
3.Заполняем таблицу:
|
|
|
|
| ||
|
| + | - | + | ||
|
|
|
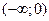
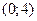
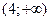
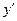
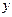
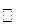
| -27 |
| |
| max | min |
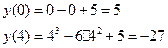
Таким образом, х=0 – точка максимума, х=4 – точка минимума, а экстремумы функции равны: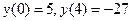 
.
Ответ: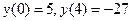
Пример 3. Найти асимптоты графика функции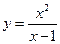 
.
Решение: Функция непрерывна везде, кроме х=1, т.е.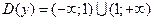 
.
1. Проверим, есть ли горизонтальные асимптоты.
Находим:
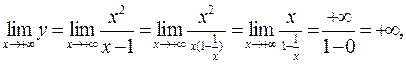
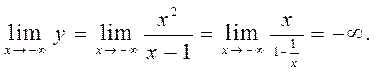
Отсюда следует, что горизонтальных асимптот график функции не имеет.
2. Проверим, есть ли вертикальные асимптоты.
Разрыв функции возможен только при х=1. Так как 
а
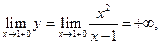то прямая х=1 – вертикальная асимптота. Других вертикальных асимптот нет, так как они находятся только либо в точках разрыва, либо на концах
её области определения.
3. Проверим, есть ли наклонные асимптоты.
Находим: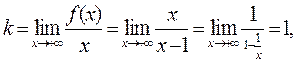 
(аналогично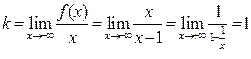 
);
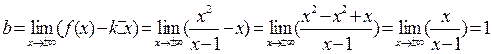
Следовательно,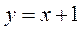 
- наклонная асимптота.
Ответ: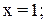 
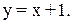
Пример 4. Провести полное исследование функции 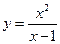и построить её график.
Решение:
1. 
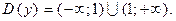
2. Разрыв функция имеет в точке х=1, так как ни левосторонний предел, ни правосторонний предел не существует, т.е.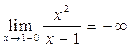 
, 
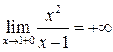. (см.пример 3)
3. Функция непериодическая. Исследуем на четность и нечетность:
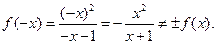
Следовательно, данная функция ни четная, ни нечетная (т.е. общего вида).
4. Найдем точки пересечения с осями координат.
С осью ОУ график пересекается при х=0, а 
, т.е. О(0;0).
С осью ОХ график пересекается при у=0, а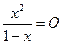 
при х=0, т.е. О(0;0).
Следовательно, О(о;о) – единственная точка пересечения функции с осями ОХ и ОУ.
5. Найдём все асимптоты график (см.пример 3)
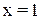- вертикальная асимптота, 
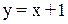- наклонная асимптота.
6. Найдём интервалы монотонности и экстремумы функции:
1. 
.
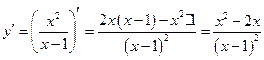2. х=0, х=2, х=1 – критические точки.
3. Заполним таблицу:
|
|
| 
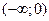
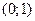
| (1;2) |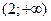 
| |||
|
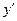
| + | - | не сущес. | - | + | ||
|
|
|
| - |
|
| ||
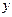
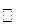
| max | min |
;
.
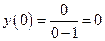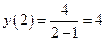Таким образом, функция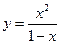 
возрастает на интервалах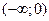 
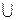
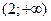, убывает на интервалах (0;1) 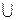(1;2). Х=0 – является точкой максимума, 
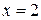- точкой минимума, а экстремумы функции: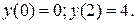 
7. Найдём интервалы выпуклости и точки перегиба.
1. 
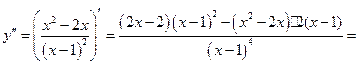
2.Исследуем при х=1.
3. Заполним таблицу:
|
| 
| 
|
| - | + |
| 
|
|
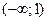
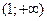
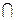
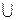
Таким образом, функция выпуклая вверх на интервале 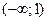и выпуклая вниз на интервале 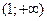. Точек перегиба нет, так как в точке х=1 – вторая производная не существует.
8. Учитывая полное исследование, строим график функции .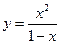
