Непрерывной называется случайная величина, которая может принимать все значения из некоторого конечного или бесконечного промежутка.
Число возможных значений непрерывной случайной величины бесконечно.
 . Расстояние, которое пролетит снаряд при выстреле из орудия – непрерывная случайная величина. Ее возможные значения принадлежат некоторому промежутку (а;b).
. Расстояние, которое пролетит снаряд при выстреле из орудия – непрерывная случайная величина. Ее возможные значения принадлежат некоторому промежутку (а;b).
Способы описания непрерывной случайной величины
1) Функция распределения.
2) Плотность распределения.
Плотность распределения вероятностей (плотность вероятности) непрерывной случайной величины X- функция f(x)- первая производная от функции распределения F(X):
F(x)=  (x).
(x).
Плотность распределения называют так же дифференциальной функцией или дифференциальным законом распределения.
График плотности распределения называется кривой распределения.
Нахождение функции распределения по известной плотности распределения.
Теорема. F(x)= 
Свойство плотности распределения.
1) f(x)  0
0
2) P(x1 
 X <x2)=
X <x2)= 
3) 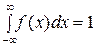
4_) P(x  X
X  <x +
<x +  x)
x) 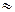 f(x)
f(x) 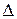 x,
x, 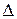 x-мало.
x-мало.
Числовые характеристики непрерывных случайных величин.
Если возможные значения непрерывной случайной величины X принадлежат [а;b], то:
Математическое ожидание M(X)= 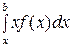 ;
;
Дисперсия D(X)= 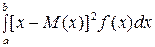 .
.
Теорема 1. D(X)= 

Если возможные значения непрерывной случайной величины X принадлежит всей оси Оx,то
M(X)= 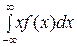 .
.
D(X)= 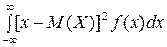 .
.
Теорема 2. D(X)=  .
.
СКО непрерывной случайной величины δ(х)= 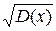
Теорема 3 Свойства математического ожидания и дисперсии дискретных случайных величин сохраняются и для непрерывных случайных велечин.
 Пример Найти математическое ожидание и дисперсию случайной величины Х, заданной функцией распределения
Пример Найти математическое ожидание и дисперсию случайной величины Х, заданной функцией распределения
0, x£0
F(x)= x, 0<x£1
1, x>1
 Решение
Решение
0, x£0
f(x)=F`(x)= x, 0<x£1
1, x>1
¥ 0 ¥ 0 1 ¥ 1 1
M(X)=òxf(x)dx=òxf(x)dx+òxf(x)dx=ò(x*0)dx+ò(x*1)dx+ò(x-0)dx=0+òxdx+0=x2/2ô=1/2
-¥ -¥ 0 -¥ 0 1 0 0
¥ 1 1
D(x)=òx2f(x)dx-[M(x)]2=òx2dx-1/4=x3/3ô-1/4=1/3-1/4=1/12.
-¥ 0 0
Основные виды распределений непрерывных случайных величин.
1) Равномерное – распределение вероятностей, при котором на интервале, которому принадлежат все возможные значения случайной величины, плотность распределения
сохраняет постоянное значение
Пример Шкала измерительного прибора проградуирована в некоторых единицах.
Ошибку при округлении отсчета до ближайшего целого деления можно рассматривать как случайную величину Х, которая может принимать с постоянной плотностью вероятности любое значение между двумя соседними делениями. Т.е. Ч имеет равномерное распределение.
 Плотность равномерного распределения на (a;b)
Плотность равномерного распределения на (a;b)
0, x£a
f(x)= 1/(b-a), a<x£b
0, x>b
M(X)=(a+b)/2; D(X)=(b-a)2/12; δ(X)=(b-a)/2 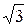
Часто в качестве интервала (a;b) берут интервал (0;1). Тогда
 0, x£0
0, x£0
f(x)= 1, 0<x£1 M(X)=1/2; D(X)=1/12; δ(X)=  =1/2
=1/2 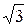 =
= 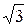 /6
/6
0, x>1
2) Нормальное - распределение вероятностей непрерывной случайной величины, которое описывается плотностью
f(x)=  e-
e- 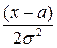
M(X)=a; D(X)=δ2; δ(X)= 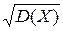 =δ
=δ
Нормальное распределение с параметрами a=0 и δ=1 называется нормированными.
Плотность нормированного нормального распределения:
Φ(x)=  e
e 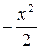 (находится по таблице)
(находится по таблице)
Функция распределения для нормального распределенной случайной величины Х:
x x
F(x)=òf(x)dx=  òe
òe  dz
dz
-¥ -¥
Функция распределения для нормированной нормально распределенной случайной величины Х:
x
F(x)=  òe
òe  dz
dz
-¥
Свойство функции F0(x): F0(x)+F0(-x)=1ÞF0(-x)=1-F0(x)
График плотности нормального распределения называется нормальной кривой (кривой Гаусса)

Свойства плотности нормального распределения.
1) D(f): xÎR
2) f(x)>0 "xÎR
3) lim f(x)=0 Þ ось 0х- горизонтальная ассимптота графика
x®±¥
4) fmax=f(a)= 
5) График функции симметричен относительно прямой х=а
6) Точки перегиба графика: x=a±δ; f(a±δ)= 
При а=0 и δ=1 нормальную кривую Φ(x)=  e
e 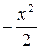 называют нормированной.
называют нормированной.
Влияние параметров нормального распределения на форму и расположение нормальной кривой.

Измерение параметра a (мат. ожидания) не изменяет формы нормальной кривой, а приводит лишь к её сдвигу вдоль оси Ох: вправо, если a возрастает, и влево, если a убывает.

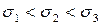
C возрастанием 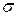 максимальная ордината нормальной кривой убывает, а сама кривая становится более пологой, т.е. сжимается к оси Ох; при убывании
максимальная ордината нормальной кривой убывает, а сама кривая становится более пологой, т.е. сжимается к оси Ох; при убывании 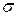 нормальная кривая становится более «островершинной» и растягивается в положительном направлении оси Оу.
нормальная кривая становится более «островершинной» и растягивается в положительном направлении оси Оу.
Вероятность попадания в заданный интервал нормальной случайной величины.
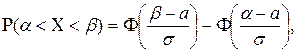 где
где  - функция Лапласа (находится по таблице).
- функция Лапласа (находится по таблице).
Пример.
Случайная величина Х распределена по нормальному закону. Математическое ожидание и СКО этой величины соответственно равны 30 и 10. Найти вероятность того, что Х примет значение, принадлежащее интервалу (10;50).
Решение.
a=30; 
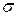 =10.
=10.
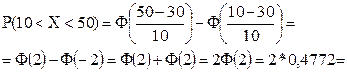
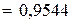
Вычисление вероятности заданного отклонения.
 (*)
(*)
Правило трех сигм.
Положим в формуле (*)  Тогда
Тогда 
Если t=3, то  и
и 

Сущность правила трех сигм состоит в том, что если случайная величина разделена нормально, то величина ее отклонения от математического ожидания по модулю не превосходит утроенного СКО.
На практике правило трех сигм применяют так: если распределение случайной величины неизвестно, но условие, указанное в правиле трех сигм, выполняется, то есть основание предполагать, что изучаемая величина распределена нормально, в противном случае она не распределена нормально.
Медиана и мода случайной величины.
Медианой Ме(Х) непрерывной случайной величины Х называется такое её значение, для которого P(X<Me(X))=P(X>Me(X))=  .
.
Геометрически вертикальная прямая x=Me(X) делит площадь фигуры под кривой разделения на две равные части. В точке x=Me(X) функция распределения равна 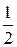 , т.е. F(Me(X))=
, т.е. F(Me(X))= 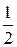 .
.
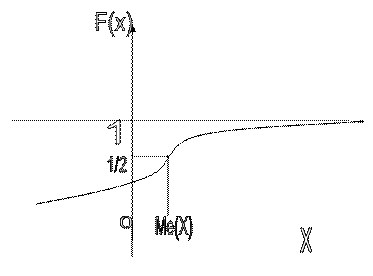

Модой М0(Х) случайной величины Х называется ее наиболее вероятное значение для которого вероятность Рi или плотность вероятности f(x) достигает максимума.
Различают унимодальные (имеющие одну моду), бимодальные (имеющие две моды) и полимодальные (имеющие несколько мод) распределения.

Неравенство Маркова.
Теорема. Д ля каждой неотрицательной величины Х, имеющей математическое ожидание М(Х) 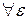 >0 справедливо соотношение:
>0 справедливо соотношение:
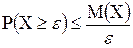 , называемое неравенством Маркова.
, называемое неравенством Маркова.
Пример. Пусть Х- время опоздания студента на лекцию, причем известно что М(Х)=1(мин.) Оценить вероятность того, что студент опоздает не менее, чем на 5 мин.
Решение. 
Неравенство Чебыщева.
Теорема. Для каждой случайной величины Х, имеющей дисперсию 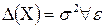 >0 справедливо неравенство Чебыщева.
>0 справедливо неравенство Чебыщева. 






