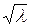Независимость случайных величин

2 случайные величины X и Y называется независимыми, если закон распределения одной из них не зависит от того, какие возможные значения приняла другая величина.

В противном случае величины зависимы.

Несколько случаных величин называются взаимно-независимыми, если законы распределения любого числа из них не зависит от того, какие возможные значения приняли остальные величины.

Действия над случайными величинами.

Суммой (разностью или произведением) случайных величин X и Y называется случайная величина, которая принимает все возможные значения вида Xi+Yi(Xi-Yi или Xi*Xj),где i= ,j= 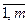, С вероятностями Pij того, что случайная величина X примет значение xi, а Y – значение yi:

Pij =P[(X=xi)(Y=ui)]

Если случайные величины X и Y называемы, т.е. независимы любые события X=xi,Y=yj, то по теорема умножения вероятностей для независимых событий Pij=P(X=xi)P(Y=yj)=PiPj

Произведением с X случайной величины X на постоянное число C называется случайная величина, которая принимает значения Cxi с теми же вероятностями Pi,i=

M – ой степенью X случайной величины X называется случайная величина, которая принимает значения Xi с теми же вероятностями Pi, I= ЛЕКЦИЯ 21.05.02.

Функции от случайных величин.

Случайная величина У, ставящая в соответствие каждому значению х случайной величины Х по некоторому правилу или закону f одно определённое значение у, называется функцией У=f(Х) от случайной величины Х.

Числовые характеристики случайной величины- числа, которые описывают случайную величину суммарно.

Числовые характеристики дискретных случайных величин.

Математическое ожидание – сумма произведений всех возможных значений дискретной случайной величины на их вероятности.

М(Х)=

Пример. Найти математическое ожидание случайной величины Х, зная её закон распределения

 

Х
Р	0,1	0,6	0,3

Решение. М(Х)= 3*0,1+ 5*0,6 + 2*0,3 = 0,3+ 3 +0,6= 3,9.

Вероятный смысл математического ожидания.

Математическое ожидание» (тем точнее, чем больше испытаний) среднему арифметическому наблюдаемых значений случайной величины.

Свойства математического ожидания

1) М(С)= С, С= const.

2) M(CX)=CM(X).

3) Математическое ожидание алгебраической суммы двух случайных величин равно такой же сумме их математических ожиданий.

М(Х ± У)=М(Х) ± М(У)

Следствие Математическое ожидание алгебраической суммы конечного числа случайных величин равно такой же сумме их математических ожиданий.

4) Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий.

М(ХУ) = М(Х)М(У)

Следствие Математическое ожидание произведения конечного числа взаимно независимых случайных величин равно произведению их математических ожиданий.

 

n n

М(ΠХi) = ПМ(Хi)

I=1 i=1

Математическое ожидание числа появлений события в независимых испытаниях

Теорема. Математическое ожидание М(Х) числа появлений события А в n независимых испытаниях равно произведению числа испытаний на вероятность появления события в каждом испытании: М(Х)=пр.

Определение. Отклонением (центрированной случайной величиной) называется разность между случайной величиной и её математическим ожиданием.

Теорема. Математическое ожидание отклонения равно 0: М(Х-М(Х))=0

Дисперсия (рассеяние) случайной величины Х – математическое ожидание квадрата отклонения случайной величины от её математического ожидания:

 

D(X)= s²=M(X – M(X))²=S(x_i – M(x_i))²P_i

Вероятностный смысл дисперсии - степень рассеяния (разброса) значений случайной величины вокруг её математического ожидания

Теорема Дисперсия равна разности между математическим ожиданием квадрата случайной величины Х и квадратом её математического ожидания:

D(X)=M(X²)-[M(X)]²

Пример 1 Найти дисперсию случайной величины Х, которая задана законом распределения,

Х
Р	0,1	0,6	0,3

Решение М(Х) = 2*0,1+3*0,6+5*0,3=0,2+1,5=3,5

1) D(x) =(2-3,5)²*0,1+(3-3,5)²*0,6+(5-3,5)²*0,3=2,25*0,1+0,25*0,6+2,25*0,3=2,25*0,4+0,15=0,9+0,15=1,05.

2) D(X)=2²*0,1+3²*0,6+5²*0,3-(3,5)²=0,4+5, 4+7,5-12,25=13,3-12,25=1,05.

Пример 2 сравнить дисперсии случайных величин, заданных законами распределения

Х	-1
Р	0,48	0,01	0,09	0,42

 

У	-1
Р	0,19	0,51	0,25	0,05

 

М(X)=-0,48+0,01+0,18+1,26=1,45-0,48=0,97

M(Y)=-0,19+0,51+0,5+0,15=1,16-0,19=0,97

D(X)=0,48+0,01+0,36+3,78-0,97²=4,63-0,9409»3,69

D(Y)=0,19+0,51+1+0,45-0,97²=2,15-0,9409»1,21

Свойства дисперсии

1) D(C) =0, C=const

2) D(CX)=C²D(X)

3) Дисперсия алгебраической суммы двух независимых случайных величин равна сумме дисперсий этих величин

D(X± Y)=D(X)+D(Y)

 

Следствие1 Дисперсия алгебраической суммы конечного числа взаимно независимых случайных величин равна сумме дисперсий этих величин

Следствие 2 D(C+X)=D(X), C=const

Дисперсия числа появлений события в независимых испытаниях

Теорема Дисперсия числа появлений события А в n независимых испытаниях, в каждом из которых вероятность Р появления события постоянна, равна произведению числа испытаний на вероятность появления и непоявления события в одном испытании:

D(X)=npq.

 

-21-

Пример. Производятся 10 независимых испытаний, в каждом из которых вероятность появления события равна 0,6. Найти дисперсию случайной величины X-числа появления событий в этих испытаниях.

Решение. n=10; p=0,6 q=1- 0,6 =0,4 D(X)=npq=10*0,6*0,4=2,4

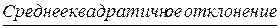(СКО) случайной величины X- квадратный корень из дисперсии:

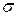(X)= .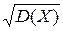

Дисперсия имеет размерность, равную квадрату размерности случайной величины X, а размерность 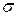(X) совпадает с размерностью (X). Поэтому в тех случаях, когда желательно, чтобы оценка рассеяния имела размерность случайной величины, вычисляют СКО, а не дисперсию.

СКО алгебраической суммы взаимно независимых случайных величин.

. СКО алгебраической суммы конечного числа взаимно независимых случайных величин равно квадратному корню из суммы квадратов СКО этих величин:

Основные виды распределений дискретных случайных величин.

_1 ) Биномиальное – распределение вероятностей, определяемое формулой Бернулли.

Биномиальный закон:

 

X	n	n-1	…	k	…
p	Pn	Npn-1q	…		…	qn

 

M(X)=np;D(X)= pqn; 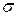(X) =

2) Пуассоновское – распределение Пуассона вероятностей массовых (n- велико) и редких (p- мала) событий.

 

P_n(k)= / k!

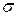M(X)=D(X)= (X)=