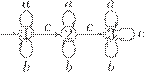
Определение 2.6.1. Конечный автомат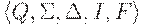 
называется детерминированным (deterministic), если
- множество I содержит ровно один элемент;
- для каждого перехода
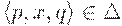выполняется равенство |x| = 1; - для любого символа
и для любого состояния 
существует не более одного состояния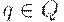 
со свойством 
.
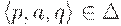Пример 2.6.2. Конечный автомат из примера 2.1.14 является детерминированным.
Определение 2.6.3. Детерминированный конечный автомат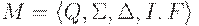 
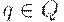называется полным (complete), если для каждого состояния и для каждого символа найдется такое состояние , что .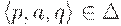
Пример 2.6.4. Конечный автомат из примера 2.1.14 эквивалентен полному детерминированному конечному автомату 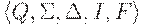, где Q = {1,2,3}, 
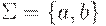, I = {1}, F = {1,2},
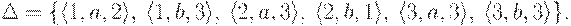
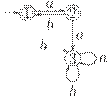
Замечание 2.6.5. Некоторые авторы используют в определении полного детерминированного конечного автомата вместо отношения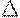 
функцию 
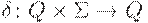. От функции 
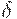можно перейти к отношению 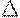, положив
Упражнение 2.6.6. Является ли детерминированным следующий конечный автомат?
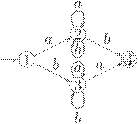
Упражнение 2.6.7. Является ли полным следующий детерминированный конечный автомат с алфавитом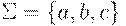 
?
