1. Сформировать ТР и подготовить ТАР
2. Выбор первой координаты сканируемой строки: у = min {ymin};
3. Если у = уmin, то перенос группы из ТР в ТАР.
Таблица активных ребер (ТАР)
| Ребро | уНАЧ | хНАЧ | ∆х | VНАЧ | ∆V |
| AB | 0.5 | ||||
| AE | |||||
| DC | 0.25 | ||||
| DE | -1 |
4. Упорядочивание ребер в ТАР по возрастанию хНАЧ.
5. Сканирование (проводят сканирующую строку).
а) переключение режимов по хНАЧ
б) учёт прохождения через вершины – локальные экстремумы. Если точка – локальный экстремум, то режим следует сохранить. Для отслеживания данной ситуации можно включить в ТР уmax, при совпадении необходим дополнительный анализ.
в) проводить линейную интерполяцию яркости при закраске от (хНАЧ , VНАЧ)i до (хНАЧ , VНАЧ)i+1
6. Удалить из ТАР те ребра, для которых справедливо у = уmax
7. Для всех элементов в ТАР произвести: хНАЧ = хНАЧ + ∆х; VНАЧ = VНАЧ + ∆V;
8. Переход к следующей сканирующей строке: y=y+1;
9. Проверка на окончание: если y>max{уmax}, то конец, иначе осуществить переход к п.3).
3. Геометрические преобразования
3.1. Координаты и преобразования
Описание, конструирование, манипулирование и представление геометрических объектов являются центральными работами в графических системах. Их поддержка в требуемом объеме за счет соответствующих математических методов, алгоритмов и программ оказывают существенное влияние на возможности и эффективность графической системы. В данном разделе будут рассмотрены математические методы для описания геометрических преобразований координат в двух и трехмерном случае, будут обсуждены некоторые вопросы эффективности, рассмотрены геометрические преобразования растровых картин.
Далее большими буквами x, y, z будут обозначаться обычные декартовые координаты, а маленькие буквы X, Y, Z будут использоваться для обозначения т.н. однородных координат.
3.2. Двумерные геометрические преобразования
Параллельный перенос

Параллельный перенос в плоском случае имеет вид:
 |
x` = x + Dx
y` = y + Dy
[x’, y’] = [x, y] + [Dx, Dy]
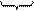 |  | 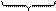 |
P’ P T
или в векторной форме:
| P` = P + T, |
где P` = [x` y`] - вектор-строка преобразованных координат,
где x, y - исходные координаты точки,
Tx, Ty - величина сдвига по осям,
x`, y` - преобразованные координаты.
P = [x y] -- вектор-строка исходных координат,
P` = [x` y`] -- вектор-строка преобразованных координат,
T = [Tx Ty] -- вектор-строка сдвига.
Масштабирование

Преобразование масштабирования относительно начала координат имеет вид:
 x` = x ·Sx
x` = x ·Sx
y` = y ·Sy или
 |
Sx 0
[x`, y`] = [x, y] ·

 0 Sy
0 Sy
 P` P
P` P
S
или в матричной форме:
| P` = P ·S, |
где Sx, Sy -- коэффициенты масштабирования по осям, а
S - матрица масштабирования
Поворот

Преобразование поворота относительно начала координат имеет вид:
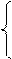 |
x`= x·cos(φ) – y·sin(φ)
y`= x·sin(φ) + y·cos(φ)
или
 cos(φ) sin(φ)
cos(φ) sin(φ)
[x`, y`] = [x, y] ·

 –sin(φ) cos(φ)
–sin(φ) cos(φ)
 P` P
P` P
R
Где R – матрица поворота
φ – положительный угол поворота
или в матричной форме:
| P` = P ·R, |
Столбцы и строки матрицы поворота представляют собой взаимно ортогональные единичные векторы. В самом деле квадраты длин векторов-строк равны единице:
| cosf·cosf+sinf·sinf = 1 |
| (-sinf) ·(-sinf)+cosf·cosf = 1, |
а скалярное произведение векторов-строк есть
| cosf·(-sinf) + sinf·cosf = 0. |
Так как скалярное произведение векторов A · B = | A | ·| B | ·cosy, где | A | - длина вектора A, | B | - длина вектора B, а y - наименьший положительный угол между ними, то из равенства скалярного произведения двух векторов-строк длины 1 следует, что угол между ними равен 90°.
Аналогичное можно показать и для векторов-столбцов. Кроме того вектора-столбцы представляют собой такие единичные векторы, которые после выполнения преобразования, заданного этой матрицей, совпадут с осями. В самом деле, произведение первого столбца на матрицу есть
 |  | ||
   
| cosf | -sinf | · | cosf | sinf | = | 1 0 | , | ||||||||||||||
| -sinf | cosf |
т.е. это единичный вектор вдоль оси X.
Аналогично, произведение второго столбца на матрицу даст вектор [ 0 1 ]. Это позволяет сформировать матрицу, если известны результаты преобразования.






