Максимизация прибыли фирмы

Задача максимизации прибыли – определение объема выпуска Q^*, при котором фирма получает максимальную прибыль. Q^*- оптимальный объем выпуска

p(Q)= [TR(Q) – TC(Q)] ® max

Условие экстремума функции p (Q):

Предположение: функция p(Q) имеет единственный экстремум – максимум

Тогда условие максимизации прибыли I порядка:

(необходимое условие)

Для максимизации прибыли фирме необходимо выбрать такой объем выпуска, при котором предельная выручка равна предельным издержкам

Eсли при некотором объеме выпуска Q

· MR(Q) > MC(Q) - для получения большей прибыли фирме следует увеличить объем выпуска;

· MR(Q) < MC(Q) - для получения большей прибыли фирме следует уменьшить объем выпуска;

· MR(Q) = MC(Q) – объем выпуска фирмы оптимален (Q = Q^*), т.е. соответствует максимальной прибыли

max p = max (TR – TC)= TR (Q^*) – TC(Q^*)

MR = tga

MC= tg b

при Q = Q^* a = b Þ MR(Q^*) = MC (Q^*)

p(0) = -FС

p(Q₁) = p(Q₂) = 0

p(Q^*) - максимальна

MR(Q^*) = MC (Q^*)

Условие I порядка – необходимое, но не достаточное для максимизации прибыли.

Если функция p(Q) имеет как максимум, так и минимум, то выполнение условия MR = MC достигается при Q = Q^* и Q = Q’, где p(Q^*) максимальна, а p(Q^э) – минимальна.

Тогда, условие максимизации прибыли II порядка (достаточное условие):

или

Графически: при оптимальном объеме выпуска Q^* тангенс угла наклона MR должен быть меньше тангенса угла наклона MC

Замечание: производные сравниваются с учетом знака, т.е. рассматривается угол наклона с положительным направлением оси Q

MR(Q^*) = MC(Q^*)

MR(Q^’) = MC(Q^’)

p(Q*) – максимальна

p(Q’) – минимальна

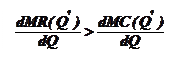
Таким образом, если при выполнении условия I порядка MR = МС

· МС возрастает, то при данном объеме выпуска достигается максимум прибыли (условие II порядка выполняется автоматически);

· МС убывает, то при данном объеме выпуска

- достигается максимум прибыли если MС пересекает MR снизу;

- достигается минимум прибыли если MC пересекает MR сверху;