Задача максимизации выпуска:
При заданной производственной функции Q(L,K), бюджете производителя С и ценах ресурсов w и r определить объемы использования ресурсов L0,K0, при которых производитель достигает максимального уровня выпуска
Q(L,K) ® max, при условии w ×L + r×K = const = C
Задача минимизации затрат:
При заданной производственной функции Q(L,K) и ценах ресурсов w и r определить объемы использования ресурсов L0,K0, при которых производитель достигает заданного уровня выпуска Q с минимальными затратами
С(L,K) ® min, при условии Q(L,K) = const = 
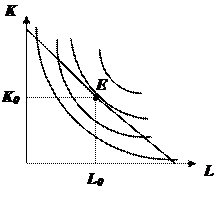
Точка равновесия (оптимума) производителя E(L0,K0) – точка касания изокосты и изокванты.
Находясь в состоянии равновесия, производитель расходует весь свой бюджет и достигает максимального уровня выпуска (или достигает заданного уровня выпуска с минимальными затратами)
Аналитически: L0 и K0 могут быть найдены как решение соответствующей системы уравнений.
Для задачи максимизации выпуска:
|
Для задачи мииимизации затрат:
