При исследовании и проектировании систем управления используют математический метод, получивший название преобразование Лапласа. Этот метод позволяет функцию одного переменного (обычно t) преобразовать в функцию другого переменного посредством соотношения:
где 
- исходная функция вещественной переменной подлежащей преобразованию по Лапласу. Эта функция называется оригиналом;
- комплексная переменная преобразования. Её называют множитель Лапласа;
- функция комплексного переменного = a +jb. Эта функция называется изображением.
Преобразование Лапласа позволяет выполнить алгебраизацию дифф. уравнений, т.е. операции дифференцирования и интегрирования заменить на алгебраические умножение и деление. После такого преобразования значительно облегчаются процессы анализа и синтеза САУ.
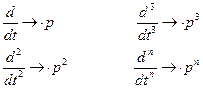
Для простейших временных функций изображения по Лапласу приведены в таблице
Таблица – изображения по Лапласу временных функций.
Примеры
1. 
2. 
3. 
(*)
Для физической реализации 
Динамические свойства систем можно оценивать по передаточным функциям, которые получают из операционных уравнений, общий вид которых представлен уравнением (*)
Передаточная функция элемента или системы представляет собой отношение изображения по Лапласу выходной величины к изображению по Лапласу входной величины при нулевых начальных условиях.
– передаточная функция
н.у. = 0
Примеры:
1. делим обе части уравнения на u(p)
2.
3. 
– передаточная функция в общем виде
