При разбивке пикетажа в вершинах углов поворота трассы измеряют горизонтальные углы b1, b2 (рис.45.1) и вычисляют углы поворота (отклонения от прямой) трассы Qлев, Qправ

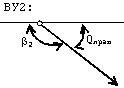
Рис.45.1. Углы поворота трассы
Qлев= b1 - 180°
Qправ= 180° - b2.
Имея углы поворота трассы и, принимая радиусы круговой кривой R согласно технических условий проектируемой дороги, вычисляют следующие основные элементы круговой кривой: тангенс (Т), биссектрису (Б), кривую (К) и домер (Д) (рис.45.2)

Рис.45.2. Элементы круговой кривой
Для вставки кривой в пикетаж определяют пикетажные наименования начала и конца круговой кривой по формулам
НК = ВУ - Т, КК = НК + К.
Результаты вычислений контролируют повторным вычисление КК
КК = ВУ + Т - Д.
Пример. Пусть R = 200 м, Q = 90° 00', ВУ ПК11+30. Необходимо определить пикетажное наименование НК и КК.
По формулам, полученным из рис. 45.2, имеем: Т = 200 . tg 45° = 200.00 м, К = 3.1416. 200. 90/180 =314.16 м, Д = 2. 200.00 - 314.16 = 85.84 м. Б = 200(1/cos45° - 1) = 82.84 м.
Вычислим НК и КК:
Расчет Контроль
ВУ ПК 11 + 30.00 ВУ ПК 11 + 30.00
-Т 2 + 00.00 +Т 2 + 00.00
НК ПК 9 + 30.00 S ПК 13 + 30.00
+К 3 + 14.16 -Д 85.84
КК ПК 12 + 44.16 КК ПК 12 + 44.16
Разбивка начала и конца круговой кривой на местности сводится к отложению расстояния 30.00 м от ПК9, и расстояния 44.16 от ПК12, сдвинутого вперед на величину домера Д = 85.84.
Контрольная работа 3. Определить положение на трассе главных точек круговой кривой (НК и КК), если: R = 200 м, ВУ ПК11+30, Q = 90° 00' - N N' (N - номер зачетной книжки).
Выполнить расчеты для выноса пикетов на кривую (п.46) и детальную разбивку кривой через 20 м.






