1. «адача. ƒоказываетс€ непосредственно из определени€ предельной точки и точной верхней грани
2. «адача. ƒанное утверждение очевидно.
3. «адача. ƒокажем неравенство по индукции. ѕри n = 2 неравенство практически очевидно. ¬ предположении индукции, что равенство верно при n докажем его при n + 1:
(1 + x) n + 1 = (1 + x) n (1 + x) ³(1 + nх)(1 + x) = 1 + (n + 1) x + nx 2³ 1 + (n + 1) x.
4. «адача. ƒоказать, что последовательность 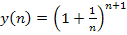 убывает и ограничена снизу. —ледовательно, она имеют общий предел c
убывает и ограничена снизу. —ледовательно, она имеют общий предел c 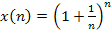 .
.
–ешение. ¬оспользуемс€ неравенством из предыдущей задачи:

ќтсюда вытекает монотонное убывание y (n). »з неравенства x (n) £ y (n) получаем ограниченность снизу.
3. «адача. ƒоказать, что limn→∞ n k/2 n = 0, limn→∞n(a 1/n− 1) = ln a, a > 0.
–ешение. (a) ƒокажем сначала дл€ k = 1. ¬оспользуемс€ биномом Ќьютона:

“огда

и 0 £limn→∞ n /2 n £limn→∞2 n /n(n Ц 1) = 0.
јналогично дл€ произвольного k:
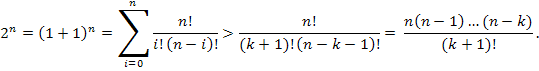
“огда

¬озможно также провести доказательство по т. Ўтольца.
(б) »сход€ из неравенства (см. замечательный предел и задачу 4)
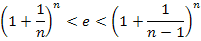
находим  . —ледовательно
. —ледовательно

ѕри а > 1 имеем 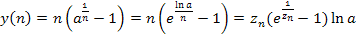 , где
, где  при
при 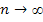 . ≈сли через a n = [ zn ] Ц обозначить целую часть zn, то a n £ zn £a n + 1 и
. ≈сли через a n = [ zn ] Ц обозначить целую часть zn, то a n £ zn £a n + 1 и  . ќтсюда вытекают неравенства
. ќтсюда вытекают неравенства


“ак как последовательность  €вл€етс€ подпоследовательностью сход€щейс€ последовательности
€вл€етс€ подпоследовательностью сход€щейс€ последовательности 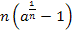 , то
, то

ѕредельный переход в полученных неравенствах доказывает утверждение. —лучай а £ 1 сводитс€ к рассмотренному переходом к b = 1/ a.
4. «адача. ѕусть limn→∞ x n = +∞. ƒоказать, что limn→∞(x1+ЈЈЈ+xn)/n= +∞.
ƒоказательство. —трогое доказательство проводитс€ по определению бесконечного предела: нам дано, что ∀M∃n1: ∀n>n1 x n> 2M и надо доказать, что ∀M∃n2: ∀n>n2¢¢(x 1+ЈЈЈ+ x n)/n>M.
¬озьмЄм n2> 2n1. “огда
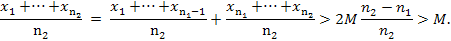
5. «адача. ѕусть∀n∈Npn> 0 иlimn→∞pn = p. ƒоказать, чтоlimn→∞(p1...pn)1/n= p.
ƒоказательство. limn→∞pn = p ⇔∀ε > 0 ∃n0 = n0(ε): ∀n > n0 |pn−p| < ε. “огда рассмотрим выражение limn→∞(p1...pn)1/n= limn→∞(p1...  )1/n limn→∞(
)1/n limn→∞( ...pn)1/n =
...pn)1/n =
= 1×limn→∞ ( ...pn)1/n. ƒл€ последнего предела в силу отмеченного выше имеем оценку:
...pn)1/n. ƒл€ последнего предела в силу отмеченного выше имеем оценку:
 £(
£( ...pn)1/n£
...pn)1/n£  .
.
“ак как limn→∞  = limn→∞
= limn→∞  = 1, по теореме о двух милиционерах получаем искомое утверждение.
= 1, по теореме о двух милиционерах получаем искомое утверждение.
6. «адача. »сход€ из равенства 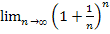 = e, доказать, что limn→∞n/(n!)1/n = e.
= e, доказать, что limn→∞n/(n!)1/n = e.
ƒоказательство. ƒокажем вспомогательное утверждение: если limn→∞yn/yn−1= a, то limn→∞  = a. ќно €вно следует из предыдущей задачи, если положить pn = yn/yn−1. “огда берЄм yn =nn/n!:
= a. ќно €вно следует из предыдущей задачи, если положить pn = yn/yn−1. “огда берЄм yn =nn/n!:

7. «адача. ƒоказать, что последовательность an = (1 + 1/n)n+p строго убывает тогда и только тогда, когда p≥ ½.
|
|
|
ƒоказательство. —равним  и
и  . ƒл€ этого сравним логарифмы этих выражений (используем монотонность функции y = ln x).
. ƒл€ этого сравним логарифмы этих выражений (используем монотонность функции y = ln x).
(n + p)(ln(n + 1) − lnn) ∨ (n + p +1)(ln(n + 2) − ln(n + 1)).
ѕусть f(x) = (x + p)(ln(x + 1) − lnx). “огда f¢(x) = (ln(x + 1) − lnx) + (x + p)  и f¢¢ =
и f¢¢ =  > 0. ѕри p ≥ ½ f¢(x) возрастает (f¢¢> 0) и limx→+∞f¢(x) = 0, то есть f¢(x) < 0 и f(x) убывает. ѕри p £ ½ f¢(x) возрастает при x<p/(1−2p) и убывает при x>p/(1−2p). limx→+∞f ¢(x) = 0, следовательно f ¢(x) > 0 при x > p/(1−2p), при таких x f(x) возрастает.
> 0. ѕри p ≥ ½ f¢(x) возрастает (f¢¢> 0) и limx→+∞f¢(x) = 0, то есть f¢(x) < 0 и f(x) убывает. ѕри p £ ½ f¢(x) возрастает при x<p/(1−2p) и убывает при x>p/(1−2p). limx→+∞f ¢(x) = 0, следовательно f ¢(x) > 0 при x > p/(1−2p), при таких x f(x) возрастает.
ƒоказано.
8.«адача. ƒоказать, что ∀r ∈ Q: |r| < 1 верны равенства 1+ r£er£ 1 + r/(1 - r).
ƒоказательство. ƒокажем левое неравенство. »звестно, что (1 + 1/x)x<e, откуда следует, что xln(1 + 1/x) < 1 ⇒ln(1+ t) <t, где t = 1/x.
“еперь докажем правое неравенство. ќно следует из того, что (1 + 1/x)x+1>e после некоторых преобразований. ¬ обоих случа€х мы брали натуральный логарифм от обеих частей неравенства и пользовались тем, что y = lnx монотонно возрастает.
10. «адача. ѕусть { x n} последовательность с ограниченным изменением, т.е. ∃c > 0: ∀n ∈ N верно неравенство 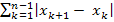 <c. ƒоказать, что последовательность { x n} сходитс€.
<c. ƒоказать, что последовательность { x n} сходитс€.
ƒоказательство. ѕусть y n  . Ёта последовательность возрастает и ограничена сверху, следовательно имеет предел. «начит дл€ неЄ выполн€етс€ критерий оши: ∀ε > 0 ∃n0 = n0(ε): ∀k,m> n0 | y k− y m| < ε
. Ёта последовательность возрастает и ограничена сверху, следовательно имеет предел. «начит дл€ неЄ выполн€етс€ критерий оши: ∀ε > 0 ∃n0 = n0(ε): ∀k,m> n0 | y k− y m| < ε
ѕо определению | x k − x m| £ | y k − y m| = | x m+1 − x m|+ ЈЈЈ+ | x k − x k−1| <ε
—ледовательно идл€ последовательности { x n} выполн€етс€ критерий оши, то есть она сходитс€.
«амечание. ѕример сход€щейс€ последовательности, не имеющей ограниченного изменени€: x n = sgn(cos(πx))×1/n.
11. «адача. ѕусть 0 £ x m+n£ x m + x n. ƒоказать, что ∃limn→∞ x n/n.
ƒоказательство. ќбозначим x n/n за y n. «аметим, что подпоследовательность {  } данной последовательности не возрастающа€ и ограниченна€ снизу, то есть сходитс€:
} данной последовательности не возрастающа€ и ограниченна€ снизу, то есть сходитс€:
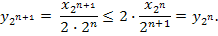
“еперь покажем, что разность между любым членом и членом с номером, равным ближайщейстепени двойки, стремитс€ к нулю, то есть и вс€ последовательность имеет предел:

12. «адача. ¬ерно ли, что
(a) 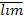 n→∞ (a n + b n) £
n→∞ (a n + b n) £ 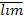 n→∞ a n +
n→∞ a n + 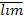 n→∞ b n, если последние пределы существуют;
n→∞ b n, если последние пределы существуют;
(b) если limn→∞ a n = a и 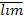 n→∞ b n = b, то
n→∞ b n = b, то 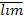 n→∞ a n b n = ab;
n→∞ a n b n = ab;
(c) 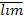 n→∞ a n = −
n→∞ a n = − 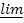 n→∞(− a n).
n→∞(− a n).
(a) ¬ыберем подпоследовательность индексов {nk}, такую, что верхний предел исходной последовательности равен пределу подпоследовательности с данными индексами. ¬ этой подпоследовательности можно выделить подпоследовательность  такую, что только последовательность
такую, что только последовательность  имеет предел, из которой уже, в свою очередь выбираем подпоследовательность
имеет предел, из которой уже, в свою очередь выбираем подпоследовательность  что
что  имеет предел. “огда каждый из верхних пределов больше соответствующего частичного предела. „то и требовалось доказать.
имеет предел. “огда каждый из верхних пределов больше соответствующего частичного предела. „то и требовалось доказать.

(b) ƒоказательство проводитс€ по аналогичной схеме.
(c) ќчевидно.
13. «адача. ѕусть limn→∞ a n = +∞. ƒоказать, что ∃minn∈N a n.
|
|
|
—читаюэтоутверждениеочевидным.
14. «адача. ѕусть limn→∞ a n = a. ƒоказать, что последовательность { a n} имеет либо наибольший, либонаименьшей элемент, либо и тот и другой.
—читаю это утверждение очевидным.
15. «адача. ѕусть s n = a 1 + ЈЈЈ + a n → ∞, a k> 0, limn→∞ a n = 0. ƒоказать, что множество предельных точек дробных частей { s n} совпадает с отрезком [0;1].
—м. задачу 29
16. «адача. ѕусть limn→∞(s n+1 − s n) = 0 и не существует ни конечного, ни бесконечного предела limn→∞ s n,и пусть l = 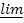 n→∞ s n, L =
n→∞ s n, L = 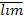 n→∞ s n. ƒоказать, что последовательность { s n} расположена всюду плотно на отрезке [ l; L ].
n→∞ s n. ƒоказать, что последовательность { s n} расположена всюду плотно на отрезке [ l; L ].
ƒоказательство. ѕокажем, что люба€ ε-окрестность точки a∈ (l; L) содержит бесконечное число элементов. —огласно условию ∃N = N(ε): | x n+1 − x n| < 2ε при n>N. ¬озьмЄм такой произвольныйε> 0, что окрестности точек l, a и L не пересекаютс€.
ѕоскольку l Ц частичный предел, то ∃ x p1 ∈Uε(l): p1 >N. јналогично ∃ x q1∈U
ε(L): q1 >N.
Ќо поскольку рассто€ние между двум€ соседними элементами при n>N меньше 2ε, то ∃ x r1∈Uε(a): p1 <r1 <q1.
ѕредполага€ далее существование таких элементов x p2∈Uε(l): p2 >p1 и x q2∈Uε(L): q2 >q1убеждаемс€, что существует и x r2∈Uε(a): p2 <r2 <q2.
ѕродолжа€ этот процесс до бесконечности, убеждаемс€ в бесконечном количестве членов последовательности, лежащих в окрестности точки a.
17. «адача.
(a) ѕусть a n> 0 и limn→∞ a n = 0. ƒоказать, что существует бесконечно много номеров n таких, что a n>max(a n+1, a n+2,...).
(b) ѕусть a n> 0 и 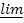 n→∞ a n = 0. ƒоказать, что существует бесконечно много номеров n таких, что a n<min(a 1, a 2,..., a n−1).
n→∞ a n = 0. ƒоказать, что существует бесконечно много номеров n таких, что a n<min(a 1, a 2,..., a n−1).
ƒанные утверждени€ более-менее очевидны, если в них хоть немного вдуматьс€.
—писоклитературы
[1] онспекты лекций по мат. анализу.
[2] √.». јрхипов, ¬.ј. —адовничий, ¬.Ќ. „убариков. Ћекции по математическому анализу, 4-е издание, исправленное. ћ.: ƒрофа, 2004. Ц 640 с.
[3] »льин ¬. ј., ѕозн€к Ё. √. ќсновы математического анализа: ¬ 2-х ч. „асть I: ”чеб.: ƒл€ вузов. Ч 7-е изд. Ч ћ.: ‘»«ћј“Ћ»“, 2005. Ч 648 с.






