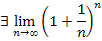
Доказательство. Докажем, что x(n) =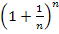 
возрастает и ограничена сверху.
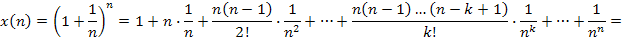
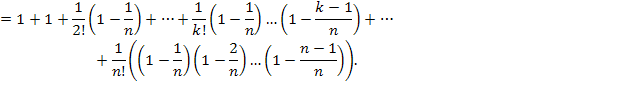
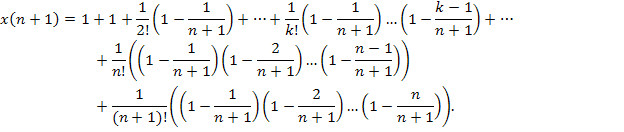
Члены x (n) меньше соответствующих членов x (n+1), к тому же в x (n+1) имеется на один член больше. Из этого следует, что x (n)< x (n+1). То есть x(n) возрастающая.
С другойстороны
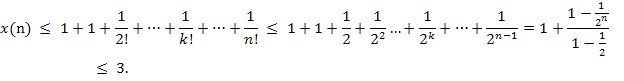
Изэтогоследует, что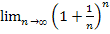 
существуети его обозначают е.
Утверждение.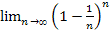 
= е -1.
Утверждение.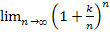 
= е k.
Утверждение. Пусть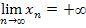 
. Тогда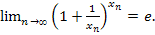 
В книге [2]: лекция 7, стр. 48-50.
6. В книге [2]: лекция 8, стр. 52-53.
7. В книге [2]: лекция 8, стр. 54.
8. В книге [2]: лекция 6, стр. 43-45; лекция 8, стр. 55.
9. В книге [2]: лекция 6, стр. 43-45; лекция 7, стр. 46-48.
Задачи
1. Пусть B – непустое ограниченное множество вещественных чисел, b = supB и bÏB. Доказать, что b является предельной точкой множества B.
2. Пусть { x n} – бесконечно малая последовательность неотрицательных вещественных чисел. Доказать, что ∀m ∈ N ∃ бесконечно много номеров n ≥ m таких, что x n£ x m.
3. Доказать, что если х > — 1, то справедливо неравенство (неравенство Бернулли)
(1 + x) n ³ 1 + nх, n > 1,
причем знак равенства имеет место лишь при х = 0.
4. Доказать, что последовательность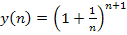 
убывает и ограничена снизу. Следовательно, она имеют общий предел c 
.
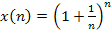3. Доказать, чтоlimn→∞ n k/2 n = 0, limn→∞n(a 1/n− 1) = ln a, a > 0.
4. Пусть limn→∞ x n = +∞. Доказать, что limn→∞(x1+···+xn)/n= +∞.
5. Пусть ∀n∈Npn> 0 и limn→∞pn = p. Доказать, что limn→∞(p1...pn)1/n= p.
6. Исходя из равенства 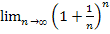= e, доказать, что limn→∞n/(n!)1/n = e.
7. Доказать, что последовательность an = (1 + 1/n)n+pстрого убывает тогда и только тогда, когда p≥ ½.
8. Доказать, что ∀r ∈ Q: |r| < 1 верны равенства 1+ r£er£ 1 + r/(1 - r).
9. Пусть { x n} последовательность с ограниченным изменением, т.е. ∃c > 0: ∀n ∈ N верно неравенство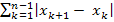 
<c. Доказать, что последовательность { x n} сходится.
10. Пусть 0£ x m+n£ x m + x n. Доказать, что ∃limn→∞ x n/n.
11. Верно ли, что
(a)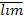 
n→∞ (a n + b n) £ 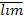n→∞ a n + 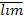n→∞ b n, если последние пределы существуют;
(b) если limn→∞ a n = a и 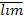n→∞ b n = b, то 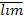n→∞ a n b n = ab;
(c) 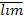n→∞ a n = − 
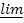n→∞(− a n).
12. Пусть limn→∞ a n = +∞. Доказать, что ∃minn∈N a n.
13. Пусть limn→∞ a n = a. Доказать, что последовательность { a n} имеет либо наибольший, либонаименьшей элемент, либо и тот и другой.
14.Пусть s n = a 1 + ··· + a n → ∞, a k> 0, limn→∞ a n = 0. Доказать, что множество предельных точек дробных частей { s n} совпадает с отрезком [0;1].
15. Пусть limn→∞(s n+1 − s n) = 0 и не существует ни конечного, ни бесконечного предела limn→∞ s n,и пусть l = 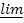n→∞ s n, L = 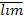n→∞ s n. Доказать, что последовательность { s n} расположена всюду плотно на отрезке [ l; L ].
16. (a) Пусть a n> 0 и limn→∞ a n = 0. Доказать, что существует бесконечно много номеров n таких, что a n>max(a n+1, a n+2,...).
(b) Пусть a n> 0 и 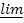n→∞ a n = 0. Доказать, что существует бесконечно много номеров n таких, что a n<min(a 1, a 2,..., a n−1).
