(а) Линейность.
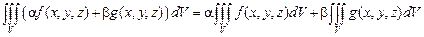
(Имеется в виду, что если существуют оба интеграла в правой части, то существует интеграл и в левой части).
(б) Аддитивность. Если область V есть объединение областей V 1и V 2,пересекающихся только по своей обшей границе,то
(Аналогично, если существуют оба интеграла в правой части, то существует интеграл и в левой части).
(в) Интеграл от константы. Двойной интеграл от константы по области V равен произведению этой константы на площадь области V 
, если C = const.
(г) Переход к неравенству. Если для всех точек 
верно неравенство f (x, y) ≤ g (x, y),то
(л) Теорема об оценке. Если числа m 1и m 2 таковы, что для всех точек 
верны неравенства m 1 ≤ f (x, y, z) ≤ m 2, то 
Определение. Средним значением функции f (x, y, z) на множестве V называется число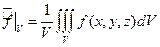 
(ж) Теорема о среднем. Если множество V замкнуто, ограниченно и связно, а функция f (x, y, z)непрерывна на множестве D, то найдется точка 
такая, что 
, т.е. такая, что 
Теорема. Если функция f (x y, z)непрерывна в кубируемой области V, то она интегрируема в этой области.
(Далее будем рассматривать только непрерывные функции).
Определение. Область V − правильная в направлении оси Oz, если:
1) всякая прямая, параллельная оси Oz, проведенная через внутреннюю (т. е. не лежащую на границе S)точку области V, пересекает поверхность S в двух точках.
2) вся область V проектируется на плоскость Оху в правильную (двумерную) область D;
3) всякая часть области V, отсеченная плоскостью, параллельной любой из координатных плоскостей (Oxy, Oxz, Oyz), также обладает свойствами 1) и 2).
Пусть поверхность, ограничивающая область V снизу, имеет уравнение 
, а поверхность, ограничивающая эту область сверху, имеет уравнение 
.
Введем понятие трехкратного интеграла IV по области V от функции трех переменных f (x, у, z), определенной и непрерывной в области V. Предположим, что область D − проекция области V на плоскость Оху − ограничена линиями
.
Определение. Тогда трехкратный интеграл от функции f (x, у, z)по области V определяется так:
