МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
РЕСПУБЛИКИ КАЗАХСТАН
НАО «АЛМАТИНСКИЙ УНИВЕРСИТЕТ ЭНЕРГЕТИКИ И СВЯЗИ»
Некоммерческое акционерное общество
«Алматинский университет энергетики и связи»
Факультет «Информационные технологии»
Кафедра «Информационные системы»
Расчетно-графическая работа №2
по дисциплине «Алгоритмизация и методы вычисления»
тема: «Решение системы линейных уравнений. Метод Зейделя»
вариант № 9
Выполнил: ст. гр. БИ-12-02
Юсупова Г. М.
Проверил: ст. преподаватель
Адилгажинова С. А.
«30» апреля 2013 г.
Алматы, 2013г.
Метод Зейделя. Одним из самых простых методов итерации является метод Зейделя. Приведем пример решения системы с помощью этого метода.
 (1.1)
(1.1)
Предположим, элементы главной диагонали системы являются ненулевыми (иначе, меняем местами уравнения). Из первого, второго и третьего уравнения системы выразим соответственно 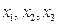 неизвестные:
неизвестные:
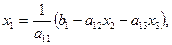 (1.2)
(1.2)
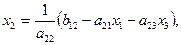 (1.3)
(1.3)
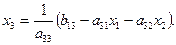 (1.4)
(1.4)
Неизвестным даем начальные (нулевые) значения: 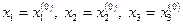 . Подставляя эти значения в правую часть уравнения (1.2) получим новое (первое) значение для
. Подставляя эти значения в правую часть уравнения (1.2) получим новое (первое) значение для  :
:
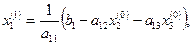
Используя это значение для  и используя значение
и используя значение 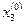 для
для  , из уравнения (1.3) получим первое значение для
, из уравнения (1.3) получим первое значение для 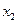 :
:

В конце, используя вычисленные значения  , при помощи уравнения (1.4) получаем первое значение для
, при помощи уравнения (1.4) получаем первое значение для  :
:
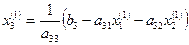
На этом первая итерация решения системы (1.2) – (1.4) закончена. Теперь используя значения 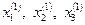 , таким же способом проведем вторую итерацию, в результате получим вторые значения:
, таким же способом проведем вторую итерацию, в результате получим вторые значения:  и так далее.
и так далее.  -е значения можно показать в таком виде:
-е значения можно показать в таком виде:

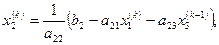
 .
.
Итерационный процесс продолжается до тех пор, пока значения  не приблизятся с заданной точностью к
не приблизятся с заданной точностью к  .
.






