ИСПРАВЛЕНИЯ К ДОКАЗАТЕЛЬСТВУ В.В. ГЛАГОЛЕВА ТЕОРЕМЫ БОУЗА-ЧАУДХУРИ В ТЕОРИИ КОДОВ, ИСПРАВЛЯЮЩИХ ОШИБКИ
Вепринцев Р.А., аспирант кафедры ПМиИ, ТулГУ
Научный руководитель: Иванов В.И., д.ф.-м.н., проф.
В учебном пособии [1] его автор известный математик В.В. Глаголев формулирует и доказывает теорему Боуза-Чаудхури. Настоящая работа содержит логически более строго доказательство этой теоремы.
Теорема Боуза-Чаудхури. Линейный код 
с проверочной матрицей
где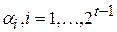 
, - ненулевые различные двоичные векторы длины 
, принадлежащие некоторому полю 
, исправляет 
ошибок.
Доказательство В.В. Глаголева. См.[1, с. 49--51].
Доказательство Р.А. Вепринцева. Обозначим столбцы проверочной матрицы 
через 
. Из теории линейных кодов известно, что двоичный линейный код исправляет ошибок, если в его проверочной матрице любые 
столбцов, рассматриваемые как элементы линейного пространства строк соответствующей длины с координатами из поля 
вычетов по модулю 2 над полем 
, линейно независимы. Возьмем в матрице любые столбцов с номерами
Обозначим
Так как элементы 
поля 
не равны нулю, то и их степени также отличны от нуля, поскольку в поле нет делителей нуля:
Допустим, что некоторая линейная комбинация выбранных столбцов равна нулю, и обозначим через 
коэффициенты этой линейной комбинации:
(1)
Отметим, что в (1) 
.
От соотношения (1) можно перейти к системе следующих соотношений:
(2)
Очевидно, что от соотношений (2) можно наоборот перейти к соотношению (1), и потому их можно назвать эквивалентными. Заметим, что в (2) 
С другой стороны, 
- ненулевой элемент поля. Пусть 
- единица поля . Если 
, то 
; при 
имеем 
. Обозначим 
через 
. Они обладают следующим свойством: 
.
Тогда получаем, что
(3)
Слева от равенства (3) элемент получается умножением элемента поля на элемент линейного пространства 
, а справа от равенства происходит умножение элементов поля по правилу, которое в нем заданно.
Поскольку в поле операция умножения элементов коммутативна, то соотношения (2) теперь можно, используя равенства (3), переписать уже в виде системы уравнений относительно неизвестных 
:
(4)
Так как - поле характеристики 2, то, возводя в четные степени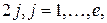 
первое уравнение системы (4) и пользуясь теорией конечных полей и соотношением , приходим к системе однородных линейных уравнений над полем , в которой неизвестных и уравнений:
(5)
Однородная система уравнений всегда совместна. Определитель системы (5) представляет собой известный определитель Вандермонда и в данном случае отличен от нуля поля . Из теории решения систем линейных уравнений [2] следует, что система совместна и имеет единственное нулевое решение 
.
Так как 
, то и 
. Таким образом, выбранные вначале доказательства столбцы матрицы линейно независимы. Следовательно, по указанному свойству линейных кодов рассматриваемый код 
исправляет ошибок, ч. т. д.
В доказательстве Глаголева существенный переход в смысле логической строгости рассуждений (3) не описан, что может привести к недоразумениям.
Также отметим в заключение, что в известных монографиях по теории кодов, исправляющих ошибки Мак-Вильямса и Слоэна, Питерсона и Уэлдона, Берлекэмпа автор не обнаружил теорему Боуза-Чаудхури.
Список литературы
1. Глаголев В.В. Алгебраическая теория кодирования. Тула: Изд-во ТулГУ, 2004. 114 с.
2. Винберг Э.Б. Курс алгебры. М.: Изд-во “Факториал Пресс”, 2001. 544 с.
