Завдання 4 ''Алгоритм комбінованої структури'': умови задачі 4 поєднують у собі циклічний (ітераційний та простий) та розгалужений алгоритми.
Завдання 5 ''Обробка масивів'': задачі 5А й 5Б містять умови задач, пов'язані з обробкою одномірних і двовимірних масивів.
1. КОНТРОЛЬНА РОБОТА 1
1.1. Завдання 1. Арифметичні вирази. Задача 1А
Таблиця 1
| № п.п. | 1А Записати арифметичні вирази в символах алгоритмічної мови | |
| sin (a 3 – 4 tg 5 / 4 (b -2)) | 
| |
log ab (2,568 c –m)5 
| arctg (x ln (3.2 a)) | |

| log 3k ( + b) + b)
| |

| n 3½ cos(2a + n 2)½5 | |
| ½0,003 а + x ln (3.2 a)½ | 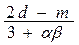 + lg (a d) + lg (a d)
| |
b a+ b am + 
| 2 ctg ½ 3 - b cos a ½ | |
| sin 4(ln (3+a) - nd)2 | 
| |
2 b+ m + 
| ½cos πam – sin 2c (b-g)½ | |
| lg ½ aa+ 2 – 2 tg (b-g)½ | 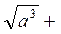 ½ ½  - d f y ½ - d f y ½
| |
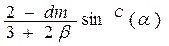
| ( + b 2) 3 + b 2) 3
| |
3,6 a 2+ k + (0,08 c – m)5 
| 3 tg 2+d (b x a - 2 j) | |
| cos 3 ½ n 2 + p ½ | 
| |
 (cos 3 a - π) (cos 3 a - π)
| 
|
Продовження таблиці 1
| № п.п. | 1А Записати арифметичні вирази в символах алгоритмічної мови | |
| ctg(3 - 6 x - b 2a+x) | sin a+k (ln (a - n d)2) | |
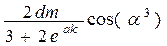
| n 3+c ½ arctg(2p+n2 ) ½ | |
| ½ 0,3e d+n +x ln (3,2 a) ½ | log n (a х) + 
| |
 tg ½ 3- cos a ½ tg ½ 3- cos a ½
| sіn n / 3 ( ) )
| |
| sin n + m (b – ln a)2 | 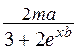 + f a m b + f a m b
| |

| c a+ m + e a +3 m | |
½ ab+c +  ½ ½
| 2 b – 3 m + 
| |

| e am + ctg (x+p) a+ m | |
| arctg½2 a + 3,06 x½2a | 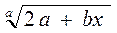 + + 
| |
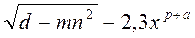
| ctg 2+a (πδa+ a ja) | |
| log b (a2 + kd)3 | 
| |
| cos5 bca – 2 ln x v y | c+3 (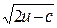 - 3mn) - 3mn)
| |
| 2 a x 4 - tg (πa+m)3 | 
| |
| ½ arctg (a + 5,2 b) 3 ½ | 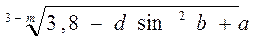
| |
0,2 х k +а(y c –m)5 
| log n+2 (p х) + 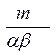
|
Продовження таблиці 1
| № п.п. | 1А Записати арифметичні вирази в символах алгоритмічної мови | |
 
| lg ½ arctg a+ 2 (b + g)½ | |
| e a+m + ctg n (3 x+p) a | sin (a b + 0,5 ctg 2a (b +3)) | |
log a-b (0,08 bc – 5)2 
| arctg (2 x ln (c+ a)) | |
| ½ a ln (3.2 + n) + 0,203 h ½ |  + lg (a c+2) + lg (a c+2)
| |

| 
| |
 ctg ½3+ cos a ½ ctg ½3+ cos a ½
| cos d+ 3 ( ) )
| |

| n 2a½ cos (2 a - n 2)½ | |
log x ( + b) + b)
| 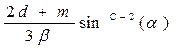
| |
| ½ cos (π+a) – sin 2 (b-g)3½ | 
| |

| t 3 dc ½ arctg (2 hp + m 2+ d )½ | |
| arctg ½2 xa + 0,25 (c + x)½2 a |  + + 
| |

|  ½ ½  - y ½ - y ½
| |

| 3 c 2c+ m - e a - 3 m | |
b a+ b am + 
| 2 ctg½3 - b cos a ½ | |

| xe am + tg 2 n (3- p) |
Продовження таблиці 1
| № п.п. | 1А Записати арифметичні вирази в символах алгоритмічної мови | |

| 
| |
| (x +2) ctg½ b - cosa ½ | 
| |
log 2n (a 3) 
| b b - a - m + 
| |

| 
| |
| sin c (ln (3 a + nd)3 | 
| |

| n (2+ d)½ cos (2 x - (3+h) n 2)½ | |
| arctg ½3 a n + x p ½2 | log ac (p х+2) + 
|
IIIIIIII
1.2. Алгоритм лінійної структури. Задача 1Б
Таблиця 2
| № п.п. | 1Б Побудувати алгоритм і написати програму |
Вычислить высоты треугольника со сторонами a, b, c
 , , 
 , где , где 
| |
Обчислити площу поверхні та об'єм усіченого конуса
 ; ; 
| |
Обчислити координати центру ваги трьох матеріальних точок з масами m1, m2, m 3 і координатами (x1,y1), (x2,y2), (x3,y3), по формулах
 , , 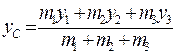
| |
Обчислити координати точки, яка ділить відрізок А 1 А 2 у співвідношенні n1: n2 по формулах
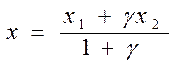 ; ;  , де , де 
| |
Обчислити медіани трикутника зі сторонами по формулах
 ; ;  ; ; 
| |
Обчислити значення функції
 , д е , д е 
|
jIIIIIIIIIIII
Продовження таблиці 2
| № п.п. | 1Б Побудувати алгоритм і написати програму |
Обчислити кутову швидкість w і доцентрове прискорення a по формулах  ; ;  ; ; 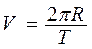
| |
Обчислити значення функції
 и и  , де , де
 ; ; 
| |
Обчислити значення функції  ,
де ,
де 
| |
Використовуючи рівняння теплового балансу, визначити питому теплоємність по формулах
 , де , де 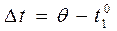
| |
Визначити коефіцієнти лінійного b і об'ємного a розширення куба з розміром грані l0 по формулах
 , , 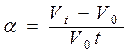
| |
Визначити питому теплоту по формулі

| |
Обчислити силу тяжіння на полюсах, екваторі й на заданій широті φ по формулах 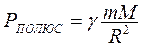 ; ; 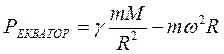 ; ; 
|
Продовження таблиці 2
| № п.п. | 1Б Побудувати алгоритм і написати програму |
Обчислити значення гіперболічних функцій (синуса, косинуса, тангенса) по формулах
 ; ;  ; ; 
| |
Обчислити значення гіперболічних функцій (арктангенса і арккотангенса) по формулах
 ; ; 
| |
Обчислити логарифм числа N по основах: a, b, 2a+b, ab по формулі 
| |
Обчислити значення арксинуса, арккосинуса, арккотангенса:
 ; ;  ; ;

| |
Перетворити декартові координати в сферичні в просторі по формулах: полярного радіуса  , довготи , довготи 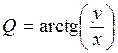 , широти , широти 
| |
Перетворити сферичні координати (полярний радіус R, довготу f, широту Q) у декартові координати по формулах  ; ;  ; ; 
| |
Перетворити полярні координати в прямокутні по формулах:
 ; ;  .
Обчислити довжину вектора D з координатами початку (x1, y1) і кінця (x2, y2) .
Обчислити довжину вектора D з координатами початку (x1, y1) і кінця (x2, y2)

|
Продовження таблиці 2
| № п.п. | 1Б Побудувати алгоритм і написати програму |
Визначити температуру звареного стику арматурних стрижнів по формулі  , де , де 
| |
Розглядається вектор у просторі з початком у точці (0, 0, 0) декартової системи координат і кінцем у точці (X, Y, Z). Обчислити його довжину D і дуги a, b, g, які він становить із осями координат  ; ;  ; ;  ; ; 
| |
Обчислити повний опір Z змінного струму, напруги UC і UL на конденсаторній котушці індуктивності по формулах
 ; ;  ; ; 
| |
Обчислити об'єм, площу повної й бічної поверхні циліндра по формулах:
 , , 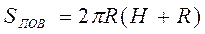 , , 
| |
Обчислити об'єм і площу поверхні кулі та кульового сегмента по формулах
 , ,  , , 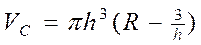 , , 
| |
Обчислити швидкості V1 I і V2 I, втрату енергії W у момент лобового зіткнення двох тіл з масами m1 і m2 по формулах 
 ; ;
 ; ;

|
Продовження таблиці 2
| № п.п. | IБ Побудувати алгоритм і написати програму |
Дані: сторона трикутника a і прилягаючі до неї кути β і γ. Визначити дві інші сторони b і c, кут між ними α по формулах
 ; ;  ; ; 
| |
Виконати перетворення декартових координат на площині при зрушенні і повороті осей координат по формулах
 ; ;
 ,
де xI и yI – нові координати точки (x,y), x и y – координати центру нової системи координат ,
де xI и yI – нові координати точки (x,y), x и y – координати центру нової системи координат
| |
Дані медіани трикутника ma, mb , mc .
Визначити площа трикутника по формулах
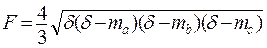 ; ; 
| |
Знайти значення середньоарифметичного температурного градієнта ΔtA та ΔtL по формулах:
 , , 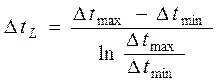
| |
Знайти площу бічної поверхні й об'єм правильної усіченої піраміди по формулах:
 , , 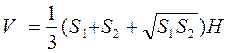
| |
Знайти радіуси вписаного й описаного кола через сторони та кути трикутника по формулах,
 
|
Продовження таблиці 2
| № п.п. | 1Б Побудувати алгоритм і написати програму |
Знайти площу прямолінійної трапеції, а також відстані центру ваги від основи a і основи b по формулах:
 , ,  , , 
| |
Знайти опір однорідних провідників при постійній і змінній температурі по формулах:
 , , 
| |
Знайти фазовий зсув і потужність змінного струму по формулах  , , 
| |
Записати формули множення й ділення двох комплексних чисел m і n:  , ,

| |
Знайти фокусну відстань двоопуклої лінзи й відстань світлової точки до лінзи по формулах,
 
| |
Обчислити суму всіх членів арифметичної та геометричної прогресії по формулах
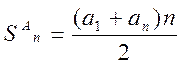 , , 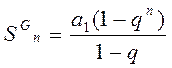
| |
Обчислити енергію зв'язку атомного ядра по формулах
 ; ; 
|
Продовження таблиці 2






