Решение квадратного уравнения

Министерство образования и науки Российской Федерации

Государственное образовательное учреждение высшего профессионального образования

«Московский государственный университет приборостроения и информатики»

 

 

Программная инженерия КБ-03

 

Домашняя работа №1

Программирование

 

 

Выполнил:

студент 1 курса

факультета КБ-03

специальности 09.03.04

Смиркин А.А.

 

Москва 2015

Лабораторная работа № 1

Решение квадратного уравнения.

 

Рассмотрим квадратное уравнение Ах² + Вх + С = 0

 

Сначала следует задать значения коэффициентов А, В, С. В разделе описания опишем А, В и С как переменные: VAR А,В,С: REAL;

Вводить значения А,В,С будем с помощью оператора ввода READLN (А,В,С);

Известно, что кор­ни квадратного уравнения вычисляются по формуле:

Несмотря на кажущуюся простоту этой формулы, воспользова­ться ею в программе без предварительного анализа нельзя, т.к. она при А = 0 теряет смысл, а при В² - 4АС<0 корни бу­дут комплексными, а ЭВМ может работать только с действительными числами. Для получения решения в общем случае нужно в алгорит­ме предусмотреть две ветви получения расписания: для случая действительных корней и для случая комплексных. В последнем случае нужно вычислить действительные и мнимые части корней.

 

Анализ показывает, что рассматриваемая задача допускает 6 вариантов решения в зависимости от численного значения коэф­фициентов:

 

А = В = С = 0 - решений бесконечно много, х - любое число;

А = В = О, С ¹ 0 - решений не существует;

А = 0; В ¹ 0 - единственное решение х = - С/В;

А ¹ 0; В² - 4АС = 0 - кратные корни х₁ = х₂ = - В/2А;

А ¹ 0; В² - 4АС > 0 - два вещественных корня:

А ¹ 0; B² - 4АС<0 - два комплексно-сопряженных корня.

 

Вариант решения с использованием оператора IF без GOTO

 

Program lab1_1;

var a, b, c, d, e, d1, x1, x2: real;

begin

writeln ('введите a, b, c'); readln (a, b, c);

if ((a=0) and (b=0) and (c=0)) then writeln ('x-любое число');

if ((a=0) and (b=0) and (c<>0)) then writeln ('решений нет');

if ((a=0) and (b<>0)) then writeln ('корень один x = ', -c/b);

d:= b*b-4*a*c;

e:= 2*a;

d1:= sqrt(abs(d));

if ((a<>0) and (d=0)) then writeln ('корни кратные x1 = x2 = ', -b/e);

if ((a<>0) and (d>0)) then

begin

writeln ('корни действительные');

writeln ('x1 = ', (-b+d1)/e);

writeln ('x2 = ', (-b-d1)/e);

end;

if ((a<>0) and (d<0)) then

begin

writeln ('корни комплексно-сопряженные');

writeln ('x1 = ', -b/e, ' -i* ', d1/e);

writeln ('x2 = ', -b/e, ' +i* ', d1/e);

end;

end.

 

 

 

 

А	В	С	результат
			x – любое число
		0,8	решений нет
			корень один x = -1.25
			корни кратные x1 = x2 = -1
			корни действительные x1 = -1, x2 = -1.5
2,3	7,65	4,2	корни действительные x1 = -0.693700064364498, x2 = -2.63238689215724
2,38	1,42	14,26	корни комплексно-сопряженные x1 = -0.298319327731092 – i * 2.42952715921381 x2 = -0.298319327731092 + i * 2.42952715921381

 

Результаты выполнения программы для варианта №9

При A = 15,1 B = 40,03 C = 201 вывод:

корни комплексно-сопряженные

x1 = -1.32549668874172 -i* 3.3991641334717

x2 = -1.32549668874172 +i* 3.3991641334717

 

Вариант решения с использованием оператора CASE без GOTO

 

Program lab1_2;

var a, b, c, d, e, d1, x1, x2: real;

begin

writeln ('введите a, b, c'); readln (a, b, c);

case ((a=0) and (b=0) and (c=0)) of

true: writeln ('x - любое число');

false:

case ((a=0) and (b=0) and (c<>0)) of

true: writeln ('решений нет');

false:

case ((a=0) and (b<>0)) of

true: writeln ('корень один x = ', -c/b);

false:

begin

d:= b*b-4*a*c;

e:= 2*a; d1:= sqrt(abs(d));

case ((a<>0) and (d=0)) of

true: writeln ('корни кратные x1 = x2 = ', -b/e);

false:

case ((a<>0) and (d>0)) of

true:

begin

writeln ('корни действительные');

writeln ('x1 = ', (-b+d1)/e);

writeln ('x2 = ', (-b-d1)/e);

end;

false:

case ((a<>0) and (d<0)) of

true:

begin

writeln ('корни комплексно сопряженные');

writeln ('x1 = ', -b/e, ' - i * ', d1/e);

writeln ('x2 = ', -b/e, ' + i * ', d1/e);

end;

end;

end;

end;

end;

end;

end;

end;

end.

 

 

 

 

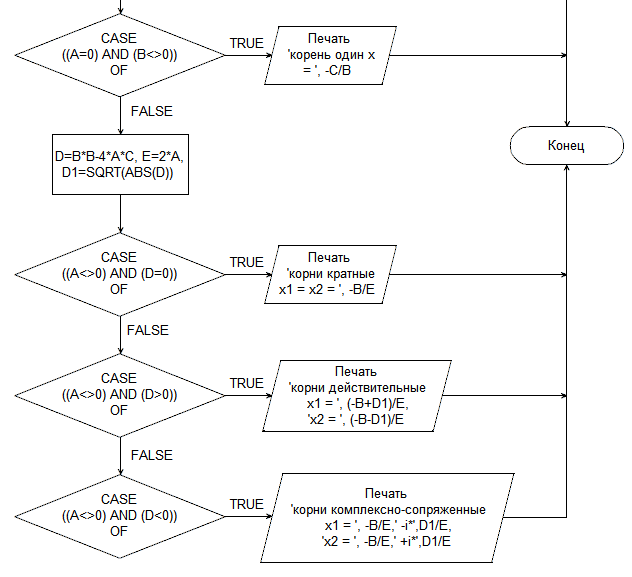
Результаты выполнения программы

 

 

А	В	С	результат
			x – любое число
		0,8	решений нет
			корень один x = -1.25
			корни кратные x1 = x2 = -1
			корни действительные x1 = -1, x2 = -1.5
2,3	7,65	4,2	корни действительные x1 = -0.693700064364498, x2 = -2.63238689215724
2,38	1,42	14,26	корни комплексно-сопряженные x1 = -0.298319327731092 – i * 2.42952715921381 x2 = -0.298319327731092 + i * 2.42952715921381

 

Результаты выполнения программы для варианта №9

При A = 15,1 B = 40,03 C = 201 вывод:

корни комплексно-сопряженные

x1 = -1.32549668874172 -i* 3.3991641334717

x2 = -1.32549668874172 +i* 3.3991641334717