Однородные дифференциальные уравнения
Однородное дифференциальное уравнение первого порядка всегда можно представить в виде
 .
.
С помощью подстановки y = и x это уравнение сводится к уравнению с разделяющимися переменными.
Пример Решить дифференциальное уравнение
 .
.
Решение. Данное уравнение является однородным дифференциальным уравнением первого порядка. Решим его с помощью подстановки.
Пусть y = и x. Дифференцируя это равенство, получим  . Подставим эти выражения в данное уравнение:
. Подставим эти выражения в данное уравнение:
 .
.
Сократим на величину и, получим уравнение с разделяющимися переменными:  .
.
Разделяя переменные и интегрируя, получим
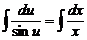 ,
, 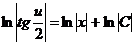
что после потенцирования дает
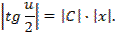
Так как
 , то
, то 
и общий интеграл имеет вид
 .
.
Задания для самостоятельного решения
Проинтегрировать уравнения:
1. 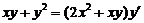 . .
| 2.  . .
|
3.  . .
| 4.  . .
|
5.  . .
| 6.  . .
|
7.  . .
| 8.  . .
|
9.  . .
| 10.  . .
|
| 11. y = x (y ' ‑ e y/x). | 12. 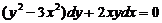 . .
|
13.  . .
| |
14. 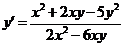 . .
| |
15.  . .
| . |
16.  . .
| 17.  . .
|
Линейные дифференциальные уравнения первого порядка
Линейным дифференциальным уравнением первого порядка называется уравнение, линейное относительно неизвестной функции и ее производной. Оно имеет вид
 ,
,
где p (x) и q (x) — заданные непрерывные функции.
Если q (x) = 0, то уравнение называется линейным однородным. Оно является уравнением с разделяющимися переменными.
Если q (x) ≠ 0, то уравнение называется линейным неоднородным. Для нахождения его решения используют метод Лагранжа (метод вариации произвольной постоянной) или метод Бернулли (метод подстановки).
Метод Лагранжа
Метод Лагранжа предполагает, что сначала находят общее решение линейного однородного уравнения
 ,
,
соответствующего данному неоднородному уравнению. Так как оно является уравнением с разделяющимися переменными, то разделив переменные и проинтегрировав, получают
 ,
,
 .
.
 ,
,
где С — произвольная постоянная.
Далее находят общее решение линейного неоднородного уравнения в виде
 .
.
Для нахождения функции С (х) подставляют y в исходное уравнение:
 ,
,
 .
.
Интегрируют, получают:
 ,
,
где С 1 — произвольная постоянная.
 .
.
Пример Найти общее решение уравнения
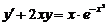 .
.
Решение. Данное уравнение является линейным неоднородным дифференциальным уравнением первого порядка, где р (х) = 2 х, q (x) =  . Решим его методом вариации произвольной постоянной.
. Решим его методом вариации произвольной постоянной.
1) Сначала решим соответствующее однородное уравнение
y ' + 2 xy = 0.
Разделяя переменные  и интегрируя, находим
и интегрируя, находим
 ,
,  или
или 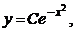 где
где  .
.
2) Найдем общее решение данного неоднородного уравнения в виде  .
.
Дифференцируя, имеем

Подставляя в данное уравнение выражения для у и y ', получим:


Отсюда
 , или
, или 
Откуда общее решение данного неоднородного уравнения: 
Метод Бернулли
Метод Бернулли предполагает, что общее решение линейного неоднородного уравнения (ищут в виде
y = u (x)× v (x),
где u (x) и v (x) — неизвестные функции от x, одна из которых может быть выбрана произвольно. Найдем эти функции.
Дифференцируем
 .
.
Подставим в уравнение (17) выражения для у и  , получим:
, получим:
 ;
;
 .
.
Так как одна из неизвестных функций, например u (x), может быть выбрана произвольно, то пусть u (x) — любое частное решение уравнения 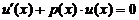 . Пусть, например,
. Пусть, например,
u (x) =  .
.
Тогда имеем уравнение 
 . Решая его, получаем вторую функцию
. Решая его, получаем вторую функцию
 .
.
Возвращаясь к переменной у, находим общее решение линейного неоднородного уравнения (17):
y = u (x)× v (x) = 
 .
.
Пример Найти общее решение уравнения  .
.
Решение. Данное уравнение является линейным неоднородным дифференциальным уравнением первого порядка. Разделив его на х, получим
р (х) = - 2/ х, q (x) =  .
.
Решим уравнение методом Бернулли.
Пусть y = u × v. Дифференцируем это выражение:  . Подставим в данное уравнение выражения для у и
. Подставим в данное уравнение выражения для у и  :
:
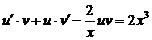 .
.
Сгруппируем члены, содержащие u в первой степени, получим 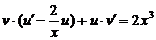 . Полагаем
. Полагаем  , откуда
, откуда  . Интегрируя, находим
. Интегрируя, находим  или
или  (постоянную интегрирования не вводим, так как достаточно найти какое-либо частное решение этого вспомогательного уравнения).
(постоянную интегрирования не вводим, так как достаточно найти какое-либо частное решение этого вспомогательного уравнения).
Для нахождения v имеем уравнение  . Это уравнение с разделяющимися переменными. Разделим его на
. Это уравнение с разделяющимися переменными. Разделим его на  :
:  . Проинтегрируем, получим
. Проинтегрируем, получим  .
.
Таким образом, общее решение данного уравнения
y = u v = 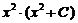 .
.
Задания для самостоятельного решения
Найти общий интеграл уравнений (1—14):
1.  3.
3.  5.
5. 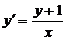 .
7. .
7.  .
9. .
9.  .
11. .
11.  .
13. .
13.  . .
| 2.  .
4. .
4.  6.
6.  .
8. .
8.  .
10. .
10.  .
12. .
12.  .
14. .
14.  . .
|
Решить задачу Коши (15—17):
15. x 2 + xy ' = y, у (1) = 0. 16. 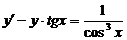 , у (0) = 0.
, у (0) = 0.
17. y' + y cos x = cos x, у (0) = 1.
Уравнение Бернулли
Дифференциальное уравнение первого порядка вида
y ' + p (x) y = q (x) ym,
где m ¹ 0, m ¹ 1, p (x) и q (x) — заданные непрерывные функции, называется уравнением Бернулли.
Пример. Найти общее решение уравнения  .
.
Решение. Данное уравнение является уравнением Бернулли, где р (х) = 1/(х - 1) = q (x),
m = 2. Решим это уравнение разными способами.
Решим уравнение методом Бернулли. Пусть y = u × v.
Дифференцируем это выражение:
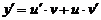 .
.
Подставим в данное уравнение выражения для у и у':
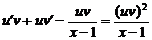 .
.
Сгруппируем члены, содержащие u в первой степени, получим
 .
.
Полагаем 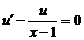 , откуда
, откуда  .
.
Интегрируя, находим  , или
, или  (постоянную интегрирования не вводим, так как достаточно найти какое-либо частное решение этого уравнения).
(постоянную интегрирования не вводим, так как достаточно найти какое-либо частное решение этого уравнения).
Для нахождения v имеем уравнение  , откуда
, откуда 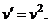 Это уравнение с разделяющимися переменными. Разделив переменные и проинтегрировав, получим
Это уравнение с разделяющимися переменными. Разделив переменные и проинтегрировав, получим 
Таким образом, общее решение данного уравнения
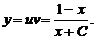
Задания для самостоятельного решения
Проинтегрировать уравнения (1—30):
1.  . .
| 2.  . .
|
3. 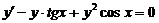 . .
| 4. 
|
5. 
| 6. 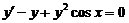 . .
|
7.  . .
| 8.  . .
|
9. 
| 10.  . .
|
11. 
| 12. 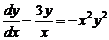 . .
|
15.  . .
| 16. 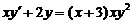 . .
|
17.  . .
| 18.  . .
|
19.  . .
| 20.  . .
|
21. 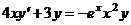 . .
| 22. 
|
23. 
| 24. 
|
25. 
| 26.  . .
|
27.  . .
| 28. 
|
29.  . .
| 30. 
|
Найти решение задачи Коши (31—36):
31. 
| 32. 
|
33. 
| 34. 
|
35. 
| 36. 
|




