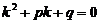Линейным однородным уравнением с постоянными коэффициентами называется уравнение вида
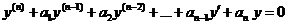 ,
,
где а 1, а 2,..., а n — некоторые действительные числа.
Для нахождения частных решений уравнения составляют характеристическое уравнение
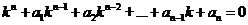 ,
,
Общее решение уравнения (строится в зависимости от характера корней характеристического уравнения по следующему правилу:
1) каждому действительному простому корню k в общем решении соответствует слагаемое вида С × е kx;
1) каждому действительному корню кратности m в общем решении соответствует слагаемое вида (С 1 + C 2 x + C 3 x 2 +... + Cm x m - 1) × е kx;
3) каждой паре комплексных сопряжённых простых корней k 1,2 = б ± в i в общем решении соответствует слагаемое вида е a x × (С 1cos b x + C 2sin b x);
4) каждой паре комплексных сопряжённых корней k 1,2 = a ± b i кратности m в общем решении соответствует слагаемое вида
е a x ((С 1 + C 2 x +... + Cmx m – 1)cos b x + (С 1 + C 2 x +... + C m x m – 1)sin b x).
Пример 1. Найти общее решение уравнения  .
.
Решение. Данное уравнение является линейным однородным уравнением третьего порядка с постоянными коэффициентами. Запишем для него характеристическое уравнение
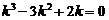 .
.
Его корни k 1 = 0, k 2 = 1, k 3 = 2 — простые действительные числа (случай 1). Следовательно, е 0× x = 1, е 1× x = е x, х · е x — частные линейно независимые решения, а общее решение данного уравнения имеет вид
у = С 1 + C 2 е x + C 3 е2х.
Пример 2. Найти общее решение уравнения 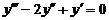 .
.
Решение. Данное уравнение является линейным однородным уравнением третьего порядка с постоянными коэффициентами. Запишем для него характеристическое уравнение
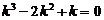 .
.
Его корни: k 1= 0 — простой действительный корень (случай 1), k 2,3 = 1 — действительный корень кратности 2 (случай 2). Следовательно, е 0× x = 1, е 1× x = е x, x × е x — частные линейно независимые решения, а общее решение данного уравнения имеет вид
у = С 1 + C 2 е x + C 3 хе2х.
Пример 3. Найти общее решение уравнения 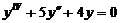 .
.
Решение. Данное уравнение является линейным однородным уравнением четвёртого порядка с постоянными коэффициентами. Запишем для него характеристическое уравнение
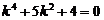 .
.
Его корни: k 1,2 = ± i, k 3,4 = ± 2 i — две пары комплексных сопряжённых простых корней (случай 3; a = 0, b = 1 для первой пары корней и b = 2 для второй пары корней). Следовательно, е 0× x × cos x = cos x, е 0× x × sin x = sin x, е 0× x × cos 2 x = cos 2 x, е 0× x × sin 2 x = sin 2 x — частные линейно независимые решения, а общее решение данного уравнения имеет вид
у = С 1 cos x + C 2sin x + С3 cos 2 x + C 4sin 2 x.
Пример 4. Найти общее решение уравнения 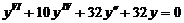 .
.
Решение. Данное уравнение является линейным однородным уравнением шестого порядка с постоянными коэффициентами. Запишем для него характеристическое уравнение
 .
.
Для нахождения корней преобразуем характеристическое уравнение к виду 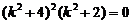 . Откуда имеем: k 1,2 = ± 2 i — комплексные сопряжённые корни кратности 2 (случай 4; a = 0, b = 2); k 3,4= ±
. Откуда имеем: k 1,2 = ± 2 i — комплексные сопряжённые корни кратности 2 (случай 4; a = 0, b = 2); k 3,4= ± 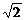 i — пара комплексных сопряжённых простых корней (случай 3; a = 0, b =
i — пара комплексных сопряжённых простых корней (случай 3; a = 0, b = 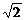 ). Следовательно, общее решение данного уравнения имеет вид
). Следовательно, общее решение данного уравнения имеет вид
у = (С 1+ C 2 x)cos 2 x + (С3 + C 4 x)sin 2 x + С5cos 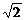 x + C 6sin
x + C 6sin 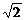 x.
x.
Выделим особо частный случай линейных однородных уравнений n - го порядка с постоянными коэффициентами (11) при n = 2, т.к. решение различных практических задач часто сводится к решению уравнений именно второго порядка.
Линейным однородным уравнением второго порядка с постоянными коэффициентами называется уравнение вида
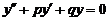 ,
,
где p, q — некоторые действительные числа.
Для практического использования указанный алгоритм оформим в виде таблицы 1.
Таблица 1. Решение линейного однородного уравнения
2-го порядка с постоянными коэффициентами
| Дифференциальное уравнение |
| ||
| Характеристическое уравнение |
| ||
| Дискриминант | D > 0 | D = 0 | D < 0 |
| Корни характеристического уравнения | k 1¹ k 2Î R | k 1 = k 2= k Î R | k 1,2 = a ± b i Î C |
| Общее решение | С 1 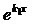 + C 2 + C 2 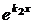
| С 1 е kx + C 2 х е kx | е a x (С 1cos b x + C 2sin b x) |
Пример 5. Найти общее решение уравнения 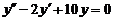 .
.
Решение. Данное уравнение является линейным однородным уравнением второго порядка с постоянными коэффициентами. Запишем для него характеристическое уравнение
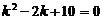 .
.
Его корни (D < 0) k 1,2 = 1 ± 3 i — комплексные сопряжённые числа (случай 3; a = 1, b = 3), следовательно, е x cos 3 x, е x sin 3 x — частные линейно независимые решения, а общее решение данного уравнения имеет вид
у = е x (С 1cos 3 x + C 2sin 3 x).
Пример 6. Найти частное решение уравнения 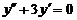 , удовлетворяющее начальным условиям: у (0) = 1,
, удовлетворяющее начальным условиям: у (0) = 1, 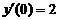 .
.
Решение. Данное уравнение является линейным однородным уравнением второго порядка с постоянными коэффициентами. Запишем для него характеристическое уравнение
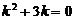 .
.
Его корни (D > 0) k 1= 0, k 2= – 3 — простые действительные числа (случай 1). Следовательно, общее решение данного уравнения имеет вид
у = С 1+ C 2 е–3х.
Дифференцируем это решение: у' = – 3 C 2 е-3х. Подставляя начальные условия в общее решение и его производную, получим систему уравнений относительно С 1и C 2:
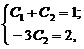
откуда С 1= 5/3, C 2 = – 2/3. Значит решение, удовлетворяющее заданным начальным условиям, имеет вид
 .
.
Проинтегрировать уравнения (1—21):
1. 
| 2. 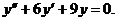 . .
|
3. 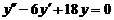 . .
| 4. 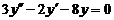 . .
|
5. 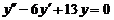 . .
| 6.  . .
|
7. 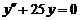 . .
| 8. 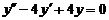 . .
|
9. 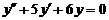 . .
| 10. 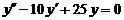 . .
|
11.  . .
| 12. 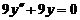 . .
|
13. 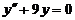 . .
| 14. 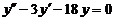 . .
|
15. 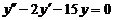 . .
| 16. 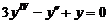 . .
|
17. 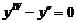 . .
| 18. 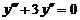 . .
|
19. 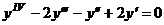  . .
| 20. 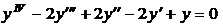 . .
|
21. 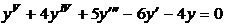 . .
|
Найти частные решения уравнений, удовлетворяющие указанным начальным условиям (22—39):
22. 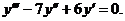
| y (0) = 0, | у' (0) = 0, | у'' (0) = 30. |
23. 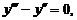
| y (0) = 0, | у' (0) = 0, | у'' (0) = – 1. |
24. 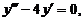
| y (0) = 0, | у' (0) = 2, | у'' (0) = 4. |
25. 
| y (0) = 0, | у' (0) = 1, | у'' (0) = 1. |
26. 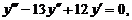
| y (0) = 0, | у' (0) = 1, | у'' (0) = 133. |
27. 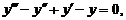
| y (0) = 0, | у' (0) = 0, | у'' (0) = 1. |
28. 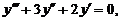
| y (0) = 0, | у' (0) = 0, | у'' (0) = 2. |
29. 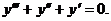
| y (0) = 0, | у' (0) = 0, | у'' (0) = 2. |
30. 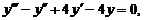
| y (0) = – 1, | у' (0) = 0, | у'' (0) = ‑ 6. |
31. 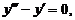
| y (0) = 0, | у' (0) = 2, | у'' (0) = 4. |
32. 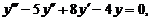
| y (0) = 1, | у' (0) = ‑ 1, | у'' (0) = 0. |
33. 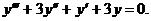
| y (0) = – 1, | у' (0) = 0, | у'' (0) = 1. |
34. 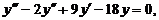
| y (0) = – 2,5, | у' (0) = 0, | у'' (0) = 0. |
35. 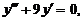
| y (0) = 0, | у' (0) = 9, | у'' (0) = ‑ 18. |
36. 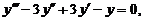
| y (0) = 0, | у' (0) = 0, | у'' (0) = 4. |
37. 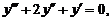
| y (0) = 0, | у' (0) = 2, | у'' (0) = ‑ 3. |
38. 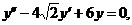
| y (0) = ‑ 3, | 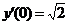
| |
39. 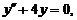
| y (р/4) = 1, | 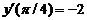
|