Занятие 8 СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
 |
Системой дифференциальных уравнений называют совокупность дифференциальных уравнений, т.е. уравнений, содержащих независимые переменные, неизвестные функции и их производные (или дифференциалы).
Система n дифференциальных уравнений первого порядка, разрешенных относительно всех производных, называется нормальной. Она имеет вид

где у 1, у 2,..., у n — неизвестные функции независимой переменной х; f 1, f 2,..., fn — известные функции, зависящие от х, у 1, у 2,..., у n, заданные и непрерывные в некоторой области.
Число уравнений, входящих в систему,называют порядком системы.
Решить систему или проинтегрировать в некотором интервале [ a, b ] — значит найти совокупность n функций у 1(х), у 2(х),..., у n (х), определённых и непрерывно дифференцируемых в указанном интервале, обращающих каждое уравнение системы в тождество.
Задача Коши для системы дифференциальных уравнений (1) состоит в нахождении решения
у 1 = у 1(х), у 2 = у 2(х),..., у n = у n (х),
удовлетворяющего начальным условиям:
 ,
, 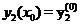 ,...,
,...,  .
.
Общим решением системы (1) называют совокупность n функций:

зависящих от переменной х и произвольных постоянных С 1, С 2,..., С n и удовлетворяющих следующим условиям:
1) функции у 1, у 2,..., у n определены в области изменения переменной х и имеют непрерывные частные производные по х;
2) функции у 1, у 2,..., у n должны являться решением системы (1) при любых значениях С 1, С 2,..., С n.
Частным решением системы называют решение, полученное из общего при некоторых частных значениях постоянных С 1, С 2,..., С n.
При решении систем часто используют следующее утверждение: cистему дифференциальных уравнений можно свести к одному дифференциальному уравнению n -го порядка:
y ( n ) = f (x, y,  ,
,  ,..., y ( n - 1)),
,..., y ( n - 1)),
и наоборот, одно дифференциальное уравнение n -го порядка можно свести к системе дифференциальных уравнений.
Система называется линейной, если неизвестные функции и их производные (или дифференциалы) входят в каждое из уравнений только в первой степени. Нормальная система линейных дифференциальных уравнений первого порядка имеет вид

где функции а ij (х), fi (х) (i = 1,..., n; j = 1,..., n) непрерывны в некотором интервале.
Если все fi (х) = 0, то система называется однородной, в противном случае — неоднородной.
Если а ij (х) = а ij = const, то система (2) называется линейной с постоянными коэффициентами.
Существуют различные методы решения систем дифференциальных уравнений. Рассмотрим простейшие из них.
Метод исключения
Метод исключения основан на следующем утверждении: нормальная система n дифференциальных уравнений первого порядка эквивалентна одному дифференциальному уравнению n —го порядка. Следовательно, можно исключить в системе все неизвестные функции, кроме одной, и получить одно дифференциальное уравнение n -го порядка.
Пример 1. Найти общее решение системы дифференциальных уравнений:

Решение. Решим систему методом исключения.
1. Дифференцируем по х любое, например первое уравнение заданной системы и подставляем вместо y ' 1, y ' 2, y ' 3 их выражения из этой системы. В результате получим
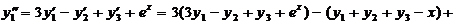

 .
.
Дифференцируем y '' 1, по х и опять заменяем y ' 1, y ' 2, y ' 3 их выражениями из системы:



Таким образом, получаем систему дифференциальных уравнений:

Из первых двух уравнений находим у 2 и у 3:

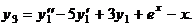
Выражения для у 2 и у 3 подставим в третье уравнение системы:
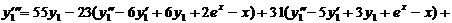


Получили неоднородное линейное уравнение третьего порядка с постоянными коэффициентами:
 .
.
Его общее решение найдём по формуле
у 1 = у 10 + у 1 *,
где у 10 — общее решение соответствующего линейного однородного уравнения;
у 1 * — частное решение линейного неоднородного уравнения
2. Найдём общее решение у 10 соответствующего линейного однородного уравнения 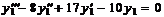 .
.
Запишем для него характеристическое уравнение
 .
.
Его корни: k 1= 1, k 2= 2, k 3= 5 — простые действительные числа. Следовательно, общее решение однородного уравнения имеет вид
у 01 = С 1 е x + C 2 е 2х + С 3 е 5х.
3. Найдём частное решение у 1 * линейного неоднородного уравнения методом неопределённых коэффициентов.
Правая часть уравнения (5) f (x) = ех – 2 х является суммой двух специальных функций
f 1(x) = и f 2(x) = – 2 х, следовательно, частным решением уравнения будет являться
у 1 * = у 1 * 1 + у 1 * 2, где у 1 * 1 и у 1 * 2 — частные решения неоднородных линейных уравнений
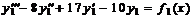 и
и  .
.
Для f 1(x) = k = 1, для f 2(x) = – 2 х k = 0, тогда получаем частное решение у 1 * линейного неоднородного уравнения:
у 1 * = А 1 x ех + А 2 x + А 3.
Найдём неизвестные величины А 1, А 2, А 3. Для этого продифференцируем три раза полученное уравнение:
 = А 1 x ех + А 1 ех + А 2;
= А 1 x ех + А 1 ех + А 2;
 = А 1 x ех + 2 А 1 ех;
= А 1 x ех + 2 А 1 ех;
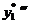 = А 1 x ех + 3 А 1 ех.
= А 1 x ех + 3 А 1 ех.
Подставим выражения для 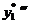 ,
,  ,
,  и у 1 * в уравнение (5):
и у 1 * в уравнение (5):
А 1 x ех + 3 А 1 ех – 8(А 1 x ех + 2 А 1 ех) + 17(А 1 x ех + А 1 ех + А 2) – 10(А 1 x ех + А 2 x + А 3) = ех – 2 x.
После преобразований получим уравнение:
4 А 1 ех + 17 А 2 – 10 А 2 x – 10 А 3 = ех – 2 x.
Приравняем коэффициенты в левой и правой частях при соответствующих выражениях, получим:
А 1 = 1/4; А 2 = 1/5; А 3 = 17/50.
Подставим эти значения в частное решение у 1 * линейного неоднородного уравнения:
у 1 * =  x ех +
x ех +  x +
x + 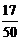 .
.
4. Таким образом, общее решение линейного неоднородного уравнения с постоянными коэффициентами (5) имеет вид
у 1 = у 10 + у 1 * = С 1 е x + C 2 е 2х + С 3 е 5х +  x ех +
x ех +  x +
x + 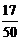 .
.
5. Найдём производные у' 1, у'' 1:
у' 1 = С 1 е x + 2 C 2 е 2х + 5 С 3 е 5х +  x ех +
x ех +  ех +
ех +  ;
;
у'' 1 = С 1 е x + 4 C 2 е 2х + 25 С 3 е 5х +  x ех +
x ех +  ех.
ех.
Подставим найденные значения у' 1, у'' 1 в равенства (4):
 = С 1 е x + 4 C 2 е 2х + 25 С 3 е 5х +
= С 1 е x + 4 C 2 е 2х + 25 С 3 е 5х +  x ех +
x ех +  ех – 6(С 1 е x + 2 C 2 е 2х +
ех – 6(С 1 е x + 2 C 2 е 2х +
+ 5 С 3 е 5х +  x ех +
x ех +  ех +
ех + 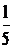 ) + 6(С 1 е x + C 2 е 2х + С 3 е 5х +
) + 6(С 1 е x + C 2 е 2х + С 3 е 5х +  x ех +
x ех +  x +
x +  ) + 2 ех – x =
) + 2 ех – x =
= С 1 ех – 2 C 2 е 2х + С 3 е 5х +  x ех +
x ех + 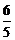 x +
x +  – ех;
– ех;
 = С 1 е x + 4 C 2 е 2х + 25 С 3 е 5х +
= С 1 е x + 4 C 2 е 2х + 25 С 3 е 5х +  x ех +
x ех +  ех – 5(С 1 е x + 2 C 2 е 2х +
ех – 5(С 1 е x + 2 C 2 е 2х +
+ 5 С 3 е 5х +  x ех +
x ех +  ех +
ех +  ) + 3(С 1 е x + C 2 е 2х + С 3 е 5х +
) + 3(С 1 е x + C 2 е 2х + С 3 е 5х +  x ех +
x ех + 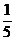 x +
x +  ) + ех – x =
) + ех – x =
= С 1 ех – 3 C 2 е 2х + 3 С 3 е5 –  x ех –
x ех –  x +
x +  ех +
ех +  .
.
Таким образом, общее решение заданной системы имеет вид
у 1= С 1 е x + C 2 е 2х + С3 е 5х +  x ех +
x ех +  x +
x + 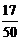 ;
;
у 2 = С 1 е x – 2 C 2 е 2х + С3 е 5х +  x ех +
x ех + 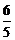 x +
x +  – ех;
– ех;
у 3 = – С 1 е x – 3 C 2 е 2х + 3С3 е 5х –  x ех –
x ех –  x +
x +  ех +
ех +  .
.
Задания для самостоятельного решения
Решить системы дифференциальных уравнений (1—15):
1. 
| 2. 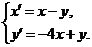
| 3. 
|
4. 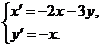
| 5. 
| 6. 
|
7. 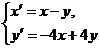
| 8. 
| 9. 
|
10. 
| 11. 
| 12. 
|
13. 
| 14. 
| 15. 
|
Решить задачу Коши для следующих систем дифференциальных уравнений (16—18):
16. 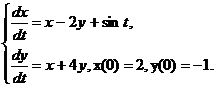
17. 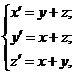 x (0) = 1; y (0) = –1; z (0) = 0.
x (0) = 1; y (0) = –1; z (0) = 0.
18. 






