Уравнения, не содержащие независимой переменной

Дифференциальные уравнения, допускающие понижение порядка

Рассмотрим простейшие виды дифференциальных уравнений, допускающих понижение порядка.

2.1.1. Уравнения вида y ⁽ ⁿ ⁾ = f (x).

Общее решение дифференциального уравнения такого вида получают n -кратным интегрированием самого уравнения:

y ⁽ ⁿ ⁾ = f (x);

;

……………………………...............

где .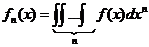

Так как являются постоянными величинами, то общее решение можно записать в виде

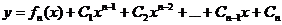Пример Найти частное решение уравнения , удовлетворяющее начальным условиям: у (0) = 1/32, , .

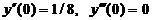Решение. 1)Найдём общее решение последовательным интегрированием данного уравнения:

;

; ;

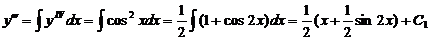2) Для нахождения частного решения необходимо определить константы С ₁, С ₂, С ₃, С ₄. Подставим начальные условия в полученные нами уравнения:

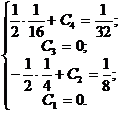
Видим, что С ₁= 0, С ₂= 1/4, С ₃= 0, С ₄= 0. Следовательно, искомое частное решение имеет вид

Уравнения, не содержащие искомой функции и производных этой функции до порядка k – 1 включительно

Уравнения, не содержащие искомой функции и производных до порядка k - 1 включительно, можно записать в виде

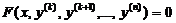. (2)

Порядок такого уравнения можно понизить на k единиц заменой , т.е. взяв за новую неизвестную функцию низшую из производных. Тогда уравнение (2) примет вид

Из последнего уравнения можно определить функцию

z = f (x, С ₁, С ₂, ..., С_{n -k}),

а затем найти у из уравнения y⁽^k⁾ = f (x, С ₁, С ₂,.., С_{n -k}) k -кратным интегрированием.

Пример Найти частное решение уравнения

удовлетворяющее начальным условиям у (2) = 1, .

Решение. Данное уравнение является дифференциальным уравнением второго порядка, не содержащим искомой функции.

1. Найдём общее решение данного уравнения. Полагая , преобразуем уравнение
к виду

Это неоднородное линейное уравнение первого порядка. Решим его методом Лагранжа.

Сначала найдём общее решение соответствующего однородного линейного уравнения первого порядка:

Для этого разделим переменные и проинтегрируем:

, где .

Затем найдём общее решение неоднородного линейного уравнения. Пусть

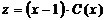Дифференцируя это равенство, получим . Подстановка z и в уравнение даёт

(x –1)∙ C' (x) = x (x – 1) C' (x) = x

Подставим последнее равенство в (4), получим общее решение неоднородного линейного уравнения (3):

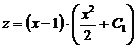Так как , получим

Это уравнение с разделяющимися переменными. Интегрируя его, получим общее решение исходного уравнения:

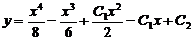2. Для нахождения частного решения необходимо определить константы С ₁, С ₂. Подставим начальные условия у (2) = 1, в полученные нами уравнения:

Решив систему, получим С ₁= –3; С ₂= 1/3. Следовательно, искомое частное решение имеет вид

Уравнения, не содержащие независимой переменной

Дифференциальные уравнения, не содержащие независимой переменной х, можно записать в виде

. (5)

Порядок такого уравнения можно понизить на единицу заменой y ' = z. При этом z рассматривается как новая неизвестная функция от у: z = z (у). Все производные 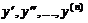выражаются через производные от новой неизвестной функции z (у):

;

и т.д.

Подставив эти выражения вместо в уравнение (5), получим дифференциальное уравнение (n – 1)-го порядка.

Пример Найти общее решение уравнения .

Решение. Данное уравнение является дифференциальным уравнением третьего порядка, не содержащим независимой переменной х.

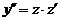
Пусть . Подставив эти выражения вместо в исходное уравнение, получим уравнение второго порядка, не содержащее независимой переменной у:

 .

Ещё раз понизим на единицу порядок уравнения. Для этого введём замену z ' = p
. Получим уравнение первого порядка с разделяющимися переменными:

Отсюда р = 0 или . Интегрируем второе уравнение :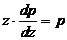
р = z C ₁.

Так как p = z ', то получим опять дифференциальное уравнение с разделяющимися переменными: z C ₁. Разделив переменные и проинтегрировав, получим .

Вводим ещё раз обратную подстановку z = y '. Получим снова дифференциальное уравнение с разделяющимися переменными:

Интегрируя его, найдём общее решение исходного уравнения:

Случай р = 0 даёт z ' = 0, откуда z = C y ' = C y = Cx + C ₄ — частное решение, которое можно получить из общего при соответствующих значениях коэффициентов С ₁, С ₂, С ₃.