Одним из основных методов интегрирования является метод замены переменной (или метод подстановки), описываемый формулой:
 (1)
(1)
Пусть заданный интеграл  не может быть непосредственно преобразован к табличному интегралу. Введем новую переменную
не может быть непосредственно преобразован к табличному интегралу. Введем новую переменную  :
:  . Тогда
. Тогда 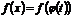 ,
,  , т.е.
, т.е.  .
.
□ Найдем производные по переменной  от левой и правой части;
от левой и правой части;  ,
,  . Т.к.
. Т.к.  , то эти производные равны, поэтому по следствию Лагранжа левая и правая части (1) отличаются на некоторую постоянную. Поскольку сами неопределенные интегралы определены с точностью до неопределенного постоянного слагаемого, то указанную постоянную в окончательной записи можно опустить.■
, то эти производные равны, поэтому по следствию Лагранжа левая и правая части (1) отличаются на некоторую постоянную. Поскольку сами неопределенные интегралы определены с точностью до неопределенного постоянного слагаемого, то указанную постоянную в окончательной записи можно опустить.■
Формула показывает, что переходя к новой переменной, достаточно выполнить замену переменной в подынтегральном выражении. Удачная замена переменной позволяет упростить исходный интеграл, свести его к табличному.
Пример. Найти  .
.
Решение.  .
.
Замечание. Новую переменную можно не выписывать явно, а производить преобразования функции под знаком дифференциала (путем введения постоянных и переменных под знак дифференциала).
Теорема. Пусть  некоторая первообразная для функции
некоторая первообразная для функции  . Тогда если вместо аргумента
. Тогда если вместо аргумента  подынтегральной функции
подынтегральной функции  и первообразной
и первообразной  подставить выражение
подставить выражение  , то это приведет к появлению дополнительного множителя
, то это приведет к появлению дополнительного множителя  перед первообразной:
перед первообразной:  , где
, где 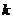 и
и  - некоторые числа,
- некоторые числа,  .
.
□ Перепишем  в виде:
в виде: 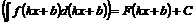 . Но
. Но  . Вынося постоянный множитель
. Вынося постоянный множитель  за знак интеграла и деля левую и правую части равенства на
за знак интеграла и деля левую и правую части равенства на  , приходим к
, приходим к  .■
.■
Алгоритм вычисления:
1) Делаем замену.
2) Дифференцируем замену  .
.
3) Под знаком интеграла переходим к новой переменной.
4) Находим табличный интеграл.
5) Возвращаемся к старой переменной.
21. Метод интегрирования по частям для случаев неопределенного и определенного интегралов (вывести формулу). Примеры.
Интегрирование - действие, обратное дифференцированию, то каждому правилу дифференцирования должно соответствовать некоторое правило интегрирования.
Пусть  и
и  - дифференцируемые функции от
- дифференцируемые функции от  х. Имеем:
х. Имеем: 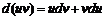 , откуда
, откуда  .
.
Интегрируя обе части последнего равенства, получим:  , или
, или
 .
.
Это и есть формула интегрирования по частям.
Интегрирование по частям состоит в том, что подынтегральное выражение  представляется каким-либо образом в виде произведения двух множителей
представляется каким-либо образом в виде произведения двух множителей  и
и  (последний обязательно содержит
(последний обязательно содержит  ) и согласно формуле данное интегрирование заменяется двумя:
) и согласно формуле данное интегрирование заменяется двумя:
1) при отыскании  из выражения для
из выражения для  ;
;
2) при отыскании интеграла от  .
.
Может оказаться, что эти два интегрирования легко осуществляются, тогда как заданный интеграл непосредственно найти трудно.
Правило интегрирования по частям нередко позволяет довести интегрирование до конца.
Пример. Найти  .
.
Решение. 
Пример. Найти  .
.
Решение. 
 .
.
Некоторые типы интегралов, берущиеся посредством формулы интегрирования по частям:
 , где , где  - многочлен - многочлен

| 
|

| 
|

| 
|






