Пример циклической задачи.

Тема 1.2. Разновидности структур алгоритмов

Ч_1. Линейные, разветвляющиеся и циклические алгоритмы.

В зависимости от особенностей своего построения ал­горитмы делятся на три основные группы:

1) линейные;

2) разветвляющиеся;

3) циклические.

 

Линейными называются алгоритмы, в которых все этапы решения задачи выполняются строго последовательно, каждая по одному разу. Линейный алгоритм состоит из команд присваивания, ввода, вывода и обращения к вспомогательным алгоритмам.

Пример.

Даны переменные А и В. Требуется обменять их значе­ния, т.е. переменная А должна получить значение В, а В — значение А.

Решение:

1. Исходные данные: А, В. Вспомогательная переменная DOP. Результат: А, В.

2. Метод решения задачи: в ЭВМ каждая величина хранится в отдельном участке памяти (переменной). Поэтому задача заключается в том, чтобы поменять местами содержимое двух ячеек.

Введем в рассмотрение еще одну величину, например С (вспомогательную). Решение задачи распадается на три этапа. Соответствующие им блоки и порядок их выполнения изображены на схеме алгоритма.

 

 

Проверим составленный алгоритм. Для этого составим трассировочную (тестирующую) таблицу, в которой будут записаны значения переменных на каждом шаге алгоритма. Пусть А=3, В=6. В итоге переменная А должна содержать 6, а переменная В – 3.

 

№	А	В	Dop
1	3	6	0
2	3	6	3
3	6	6	3
4	6	3	3

 

Результат работы алгоритма совпадает с ожидаемым. Значит, алгоритм составлен верно.

 

Разветвленными называются алгоритмы, в которых выбирается один из нескольких возможных путей вычислительного процесса. Признаком разветвляющегося алгоритма является на­личие операций условного перехода, когда происходит проверка истинности некоторого логического выражения (проверяемое условие) и в зависимости от истинности или ложности проверяемого условия для выполнения выбира­ется та или иная ветвь алгоритма. Алгоритм предполага­ет выполнение Действия 1, если записанное условие ис­тинно (выполняется), и выполнение Действия 2, если ус­ловие ложно (не выполняется).

На алгоритмическом языке команду ветвления можно записать в следующем виде:

Если условие

То серия 1

Иначе серия 2

Кв (конец ветвления)

 

В блок-схемах алгоритмов условие изображается блоком:

 

 

Пример Решение квадратного уравнения Ax ² + Bx + C =0

Циклическими называются алгоритмы, в которых часть этапов повторяется несколько раз.

Различают три вида циклов:

· Цикл с предусловием («Пока»);

На АЯ он имеет следующий вид

Пока условие, повторять

Нц

Серия

Кц

Выполнение серии команд (тела цикла) повторяется пока условие цикла истинно

           

Рассмотрим следующую задачу: дано целое положительное число n. Требуется вычислить n! (n – факториал). Вспомним определение факториала:

 

n! =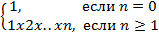

и составим алгоритм его вычисления.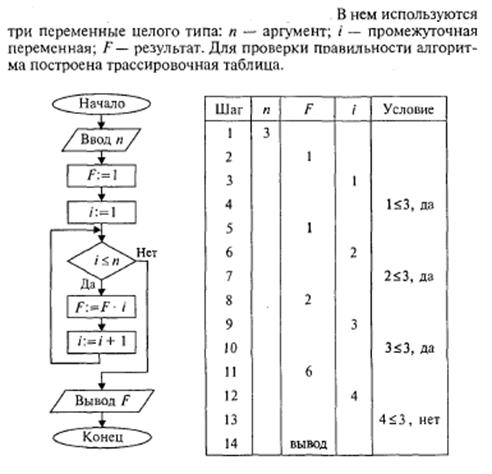

 

Данный алгоритм имеет циклическую структуру. В нем использована структурная команда цикл «ПОКА» или цикл с предусловием

 

· Цикл с постусловием («До»);

На АЯ он имеет следующий вид:

Повторять

Серия

До условие

Здесь используется условие окончания цикла, т.е. когда оно становится истинным, цикл заканчивает работу.

 

 

Составим блок схему для этой задачи, используя цикл с постусловием («До»)

    начало

 

       вводN

 

    F:=1

 

    I:=1

 

   F:=F*i

 

   I:= I+1

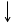да

           i≤n

                нет

    печать F

 

 

        конец

 

Цикл с предусловием (ПОКА)                        Цикл с постусловием  (ДО)

 

 

                                      нет   

 

 

                       да

                                                                                                                       нет

 

 

                                                                                                            да

 

 

В циклах с предусловием и с постусловием управляющие переменные могут изменяться с любым шагом, в цикле с параметром шаг изменения переменной по умолчанию равен 1.В любом виде цикла используется управляющая переменная. От её значения зависит, надо ли продолжать действия в цикле. До начала цикла она принимает начальное значение, а потом в цикле изменяется с шагом, который определяется условием задачи.

Шаг изменения переменной – это разность между следующим и предыдущим значениями переменной. Для циклов с предусловием и постусловием используются одинаковые действия:

- до цикла задать управляющей переменной (и, если по условию задачи нужно, то и другим переменным) начальное значение;

- выполнить действия;

- проверить условие окончания работы цикла;

- если цикл продолжает работу, то изменить значения управляющей и других переменных, использующихся в цикле. 

Различие в работе этих циклов – в порядке следования действий.

 

· Цикл с параметром.

содержит специальную переменную (счетчик, параметр цикла), которая последовательно изменяет свое значение от заданного начального до конечного значения с некоторым шагом, при этом для каждого значения счетчика тело цикла исполняется один раз

 

Пример циклической задачи.

Посчитать значения функции Y=5x² +6 для значений х = 3,4,5,…,20. Все значения вывести на экран.

Задачу можно решить тремя видами цикла: с предусловием (когда условие стоит перед действием), с постусловием (когда условие стоит после действия) и с параметром. В цикле с параметром всегда известно количество повторений или начальное и конечное значения переменной х. Шаг изменения переменной в этом цикле всегда равен 1(-1).

 

 

1) Цикл с предусловием

 

2) цикл с постусловием

 

 

3) цикл с параметром

В управляющем блоке указываются начальное и конечное значения управляющей переменной, а шаг изменения указывают, когда он равен –1 и не указывают, если он равен +1.