1.Определить числовое значение периодов Т1 и Т2 по формуле 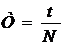 в первом и втором экспериментах для математического и физического маятников.
в первом и втором экспериментах для математического и физического маятников.
2.Вычислите среднее значение периодов математического и физического маятников по формуле 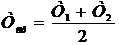
3.Измерьте приведенную длину L в каждом эксперименте и вычислите ее среднее значение.
4. Полученные данные внесите в таблицы 2.4 и 2.5
5.Сделайте вывод о периоде колебаний физического и математического маятников.
Контрольные вопросы
1. Дайте определение математического маятников.
2. Назовите формулу для вычисления периода колебаний физического маятника.
3. От чего зависит и от чего не зависит период колебаний математического маятника?
4. Что называется физическим маятником?
5. Назовите формулу для вычисления периода колебаний физического маятника.
6. От чего зависит и от чего не зависит период колебаний физического маятника?
7.Что такое точка подвеса маятника?
8. Что такое центр тяжести? Что такое центр масс?
9.Сформулируйте понятие приведенной длины физического маятника и назовите определяющую ее формулу.
10.Что означает выражение «маятники синхронны»?
Лабораторная работа №3
Тема: Определение момента инерции физического маятника
Цель: научиться определять момент инерции физического маятника
Оборудование: физический маятник (картонная пластинка), штатив с отвесом, математический маятник, линейка, секундомер, электронные весы.
Краткие теоретические сведения
Моментом инерции материальной точки относительно оси вращения называется произведение массы этой точки на квадрат расстояния от оси:
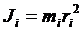 ; (2.15)
; (2.15)
Моментом инерции системы (тела) относительно оси вращения называется физическая величина, равная сумме произведений масс п материальных точек системы на квадраты их расстояний до рассматриваемой оси:
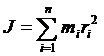 (2.16)
(2.16)
В случае непрерывного распределения масс эта сумма сводится к интегралу 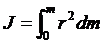 , где интегрирование производится по объему тела, т.е
, где интегрирование производится по объему тела, т.е 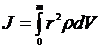
Главный момент инерции — момент инерции относительно главной оси вращения проходящей через центр масс.
Момент инерции тела зависит от того, относительно какой оси оно вращается и как распределена масса тела по объему.
Таблица 2.6 - Моменты инерции однородных тел массой m, имеющих правильную геометрическую форму и равномерное распределение массы по объему
| Тело | Положение оси вращения | Момент инерции |
| Полый тонкостенный цилиндр радиуса R | Ось симметрии | 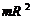
|
| Сплошной цилиндр или диск радиуса R | Ось симметрии | 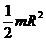
|
| Прямой тонкий стержень длиной l | Ось перпендикулярна стержню и проходит через его середину | 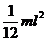
|
| Шар радиусом R | Ось проходит через центр шара | 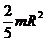
|
Если известен момент инерции тела относительно оси, проходящей через его центр масс, то момент инерции относительно любой другой параллельной оси определяется теоремой Штейнера: момент инерции тела J относительно произвольной оси z равен сумме момента его инерции Jс относительно параллельной оси, проходящей через центр масс С тела, и произведения массы m тела на квадрат расстояния a между осями:
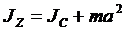 (2.17)
(2.17)
Например, момент инерции прямого тонкого стержня длиной l относительно оси, которая перпендикулярна стержню и проходит через его конец (эта ось отстоит на l /2 от оси, проходящей через центр стержня):
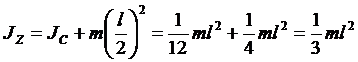
Таким образом, величина момента инерции зависит от выбора оси вращения.
При малых углах отклонения (Рис.2.4) физический маятник также совершает колебания, близкие к гармоническим, с периодом

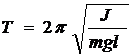
где l –расстояние от точки подвеса О до центра масс С;
m − масса тела;
J – момент инерции относительно оси, проходящей горизонтально через точку подвеса О, отсюда
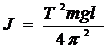 (2.18)
(2.18)
Расстояние L, между точкой подвеса и О и центром качания О/ (Рис.2.4), называют приведенной длиной физического маятника.
 ,
,
где J – момент инерции физического маятника;
m – масса маятника;
l – расстояние от точки подвеса до центра масс точки С, отсюда
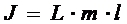 (2.19)
(2.19)
Порядок выполнения работы
Задание. Определение момента инерции физического маятника
1. Взвешиванием на весах определите массу физического маятника, полученные данные занесите в таблицу 2.7
2.На физическом маятнике измерьте расстояние от точки подвеса (О) до центра масс (С) l =ОС и занесите в таблицу 2.7
3.Период (Тср) физического маятника и приведенную длину L=ОО/ для маятника возьмите из таблицы 2.5 лабораторной работы 2.2.
Таблица 2.7 − Экспериментальные данные
| Физический маятник | |||||||||
| m, кг | l =ОС, м | Т, c | L=ОО/, м | J1,
кг 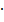 м 2 м 2
| J2, кг·м2 | Jср, кг·м2 | ΔJ, кг·м2 | ΔJср, кг·м2 | ε, % |






