Для вычисления производной неявной функции придадим x приращение Δx, тогда значение y= f(x) получит приращение Δy= f(x+ Δx) – f(x). При этом полное приращение функции F(x, y) будет равно нулю (т. к. F (x, f(x)) = 0). Но полное приращение равно 
, следовательно, Отсюда вытекает, что 
.
93. Какой вид имеет дифференциальное уравнение первого порядка?
Дифференциальными уравнениями называются уравнения, содержащие неизвестную функцию и её производные различных порядков. Если функция зависит от одного переменного, то дифференциальное уравнение называется обыкновенным. Порядком уравнения называется высший порядок, входящей в него производной. Уравнение первого порядка имеет либо вид F(x, y, y′) = 0, либо вид y′ = f(x, y).
94. Что является решением дифференциального уравнения?
Решением дифференциального уравнения первого порядка F(x, y, y′) = 0 называется функция у = φ(х) такая, что F(x, φ(х), φ′(х)) = 0. В наиболее простом случае дифференциальное уравнение первого порядка имеет вид y′ = f(x). Его решение даётся интегралом 
. Здесь с – параметр, каждое конкретное значение которого определяет конкретную функцию. Решение с неопределённым значением параметра с называется общим, а каждая конкретная функция – частным решением. Это даёт основание предполагать, что общее решение дифференциального уравнения вида F(x, y, y′) = 0 также зависит от параметра: у = φ(х, с). Выбирая различные значения параметра с, можно получить частные решения, удовлетворяющие различным начальным условиям. Например, часто требуется, чтобы кривая у = φ(х, с) проходила через заданную точку (х0; у0). Таким образом, параметр с определяют из условия у0 = φ(х0, с).
95. Какой вид имеет и как решается уравнение с разделяющимися переменными?
Уравнения с разделяющимися переменными называются уравнения вида 
. Учитывая, что 
можно записать это же уравнение в виде f(x) dx = g(y) dy. Предположим, что решением такого уравнения является заданная неявно функция F(x, y) = C. Продифференцируем её и получим выражение 
. Имея ввиду равенство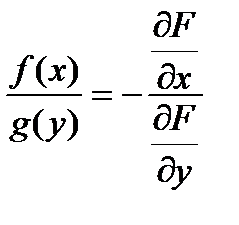 
, можно предположить, что 
зависит только от х, а 
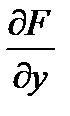зависит только от у. Можно догадаться, что функция F(x, y) имеет вид F1(x) + F2(y). Если это так, мы имеем два равенства 
= f(x) и 
= – g(y), которые позволяют найти функции F1(x) и F2(y). Очевидно, что 
и 
. В итоге формула решения уравнения с разделяющимися переменными имеет вид 
.
96. Что такое линейное однородное дифференциальное уравнение?
Линейное однородное дифференциальное уравнение имеет вид a0z(n) + a1z(n–1) +… + an–1z′ + anz = 0. Его характеристическим многочленом называется выражение L(p) = a0pn + a1pn–1 +… + an–1p + an.
97. Как получить решение однородного линейного дифференциального уравнения?
Предположим, что характеристический многочлен L(р) не имеет кратных корней. Обозначим его корни через λ1, λ2, …, λn. Тогда функции z1 =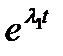 
, z2 = 
, …, zn = 
является решением исходного дифференциального уравнения, а любое другое решение этого уравнения имеет вид z = с1 z1 + с2 z2 + … + сn zn.
98. Что такое бесконечный ряд?
Пусть задана бесконечная последовательность чисел 
. Составленный из этих чисел символический ряд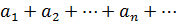 
называется бесконечным рядом, а сами числа членами ряда. Суммы вида 
называются частичными суммами. Суммой ряда 
называется конечный или бесконечный предел 
. Если предел конечен, то ряд называется сходящимся, в противном случае расходящимся.
99. Каковы условия сходимости бесконечных рядов?
Пусть даны ряды 
и 
. Если с некоторого места выполняется условие 
, то из сходимости второго ряда вытекает сходимость первого. И, наоборот, из расходимости первого ряда вытекает расходимость второго. Если существует 
, то выполняются условия предыдущего утверждения. Сравнивая произвольный ряд с рядом стандартным, например, с геометрической прогрессией, можно получить признаки сходимости рядов.
100. Каковы признаки сходимости бесконечных рядов?
Признак Коши: если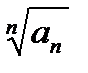 
стремится к числу q < 1, то ряд сходится. Признак Даламбера: если отношение 
стремится к числу q < 1, то ряд сходится.
