Привести примеры переменных в реальной жизни.
Универсальная переменная – время (с ней связаны любые изменения). Температура, расстояние, скорость, вес.
Привести примеры функций в реальной жизни.
Зависимость температуры от времени.
6. Для чего нужны функции?
Для описания реальных процессов.
7. Какие числовые значения принимает переменная величина?
Значениями переменных величин являются действительные (или вещественные) числа.
8. Что такое действительные числа?
Действительные числа – это рациональные и иррациональные числа.
9. Что представляют собой рациональные числа?
Рациональные числа или обыкновенные дроби представляют собой отношение вида  , где p и q целые числа. Исходной операцией, приведшей к возникновению понятия рационального числа, является дробление целого предмета на равные доли.
, где p и q целые числа. Исходной операцией, приведшей к возникновению понятия рационального числа, является дробление целого предмета на равные доли.
10. Какие формы могут иметь рациональные числа?
Обыкновенная дробь и конечная или бесконечная периодическая десятичная дробь. Примеры:  и
и 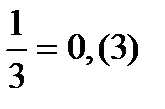 .
.
11. Как перевести обыкновенную дробь в десятичную?
Разделить p на q углом.
12. Как перевести бесконечную периодическую десятичную дробь в обыкновенную?
Найти сумму бесконечной геометрической прогрессии. Пример: 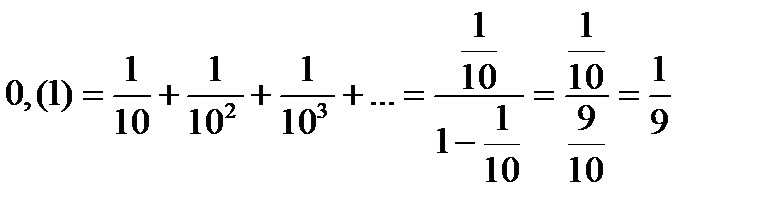 .
.
13. Что такое иррациональное число?
Бесконечная непериодическая десятичная дробь.
14. Результатом какого процесса стало понятие иррационального числа?
Результатом измерения отрезков. Впервые существование иррациональных чисел было доказано при измерении гипотенузы равнобедренного прямоугольного треугольника с единичным катетом. Таким образом,  иррационален.
иррационален.
15. Как происходит процесс измерения?
Единичный отрезок укладывается в измеряемый отрезок. Его остаток, меньший единицы, измеряется десятыми долями единичного отрезка. Новый остаток измеряется сотыми долями единичного отрезка и т. д. В результате процесс либо оборвётся и будет получена конечная дробь, либо процесс не оборвётся и будет получена бесконечная дробь. Бесконечная дробь будет либо периодической, либо непериодической. В любом случае результатом измерения будет либо рациональное, либо иррациональное число.
Привести примеры иррациональных чисел.
Число π, число е, не извлекающиеся квадратные корни из целых чисел.
17. Что такое числовая прямая?
Фиксируем на прямой точки 0 и 1. Тем самым будет задан единичный отрезок. С его помощью можно измерить расстояние от точки 0 (начало координат) до произвольной точки М. Длина отрезка 0М (с учётом знака) называется координатой точки М. Каждая точка числовой прямой связана с действительным числом – координатой точки.
18. Как следует представлять себе множество действительных чисел?
Как множество точек числовой прямой.
19. Как можно представлять себе переменную?
Как точку, движущуюся по числовой прямой. Её координата является значением переменной. Прообразом такой модели является градусник. Шкала – аналог числовой прямой, а конец столбика ртути – движущаяся точка.
20. Что такое декартова система координат?
На плоскости располагаются две перпендикулярных числовых прямых Х и Y. В результате каждая точка плоскости получает две координаты – абсциссу (х) и ординату (у). Абсцисса – расстояние от точки до оси Y (с учётом знака). Ордината – расстояние от точки до оси Х (с учётом знака).
21. Какая связь существует между понятием функции и декартовой системой координат?
Функция – это зависимость между двумя переменными. Декартова система координат позволяет совместить геометрический образ двух переменных.
22. Что такое геометрическая модель функции?
Функция – это зависимость между двумя переменными. Каждому значению абсциссы х соответствует единственное значение ординаты у. С другой стороны пара (х; у) задаёт точку на плоскости. Множество всех таких точек является некоторой кривой, называемой графиком функции.
23. Какие свойства функции можно выявить, изучая график функции?
| b |
| x |
| y |
| 0 |
24. Что представляет собой линейная функция, и каким уравнением она задаётся?
Графиком линейной функции является прямая. Выведем уравнение линейной функции. Пусть у = f(x) и пусть f(0) = b. Для любого значения х отношение приращения функции y – b к х равно тангенсу угла наклона прямой, то есть постоянно. Пусть тангенсу угла наклона прямой равен k, тогда для любой точки (х; у) верно уравнение 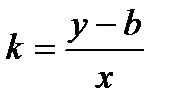 . Отсюда следует, что уравнение прямой имеет вид у = kх + b.
. Отсюда следует, что уравнение прямой имеет вид у = kх + b.
25. Какой геометрический смысл имеет коэффициент k?
Как установлено при выводе уравнения, k является тангенсом угла наклона графика линейной функции.
26. Каковы условия возрастания, убывания и постоянства линейной функции?
Если k > 0, линейная функция возрастает. Если k < 0, линейная функция убывает. Если k = 0, линейная функция постоянна.
27. Каково уравнение прямой, имеющей заданный угол наклона и проходящей через заданную точку?
Пусть прямая имеет угол наклона α и проходит через точку (х0; у0). Пусть при этом tg α = k. Уравнение прямой имеет вид 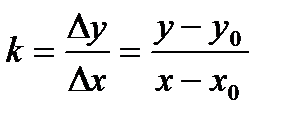 .
.
28. Как приближённо определить направление кривой на плоскости и зачем нужно его определять?
Понятие направления связано с прямой. При движении по кривой направление всё время меняется. Можно говорить только о направлении кривой в некоторой точке. На маленьком участке кривая близка к прямой. Таким образом, приблизительно направление кривой можно задать, взяв на кривой две близких точки и проведя через них прямую. Направление графика функции позволяет определить возрастает или убывает функция в данной точке.
29. Что такое секущая?
Секущая – это прямая проходящая через две точки, лежащие на кривой.
30. Каков тангенс угла наклона секущей?
Секущая проходит через две точки М0 (х0; у0) и М(х; у), лежащие на кривой. Тангенс её наклона равен 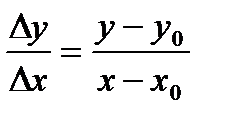 .
.
31. Что такое касательная?
Касательная – это предельное положение секущей при слиянии двух точек в одну, то есть при стремлении точки М0 к М.
32. Каков тангенс угла наклона касательной?
Тангенс угла наклона касательной равен 
33. Что такое предел?
Предел функции в точке х0 – это число, к которому приближается её значение при приближении значения аргумента к х0.
34. Каково определение непрерывности функции в точке?
Функция непрерывна в точке х0, если  , то есть непрерывная функция стремится к своему значению.
, то есть непрерывная функция стремится к своему значению.
35. Что такое производная?
Производная – это предел отношения приращения функции к приращению аргумента при стремлении приращения аргумента к нулю.
36. Каков геометрический смысл производной?
Производная равна тангенсу наклона касательной к графику функции в данной точке.
37. Каков механический смысл производной?
Производная равна скорости изменения функции в данной точке, если аргумент рассматривается как время.
38. Для чего используется производная?
Производная используется для исследования функции. Если производная функции в точке больше нуля, то функция возрастает. Если производная функции в точке меньше нуля, то функция убывает. Если производная функции в точке равна нулю, то, возможно, функция имеет в точке экстремум.
39. Что такое экстремум?
Говорят, что функции имеет экстремум в точке, если значение в этой точке больше (максимум) или меньше (минимум) любого значения той же функции в её окрестности.
40. Что такое точка перегиба?
В точке перегиба функция имеет производную, равную нулю, но не имеет экстремума.
41. Как отличить точку перегиба от экстремума?
При прохождении через точку перегиба производная не меняет знак. При переходе через точку максимума производная меняет знак с плюса на минус. При переходе через точку минимума производная меняет знак с минуса на плюс.
42. Как использовать производную при построении графика непрерывной функции?
Нужно вычислить производную и найти предполагаемые экстремумы, то есть точки, в которых производная равна нулю. Проверкой того, сменяет ли производная в этих точках знак, выделяем среди этих точек экстремумы. Вычисляем значения функции в этих точках, намечаем экстремальные изгибы и соединяем эти дуги в единый график.
43. Как найти производную сложной функции?
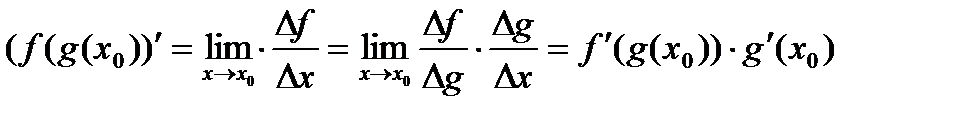 .
.
44. Что такое обратная функция, и какова её производная?
Пусть задана функция y = f(x). Функция х = f-1(у) называется обратной к ней если f(f-1(х)) = х. Продифференцируем обе части последнего равенства и получим выражение (f(f-1(х)))′ = f′(f-1(х))∙(f-1(х))′ = 1. Следовательно,  . Например, рассмотрим обратную к синусу функцию y = arctg x. Отметим, что у – угол, а х – синус, значит,
. Например, рассмотрим обратную к синусу функцию y = arctg x. Отметим, что у – угол, а х – синус, значит,  – косинус. Таким образом,
– косинус. Таким образом, 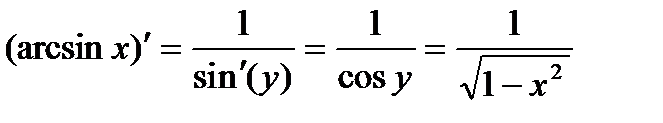 .
.
45. Как найти производную произведения двух функций?
| u(x) |
| v(x) |
| ∆v |
| ∆u |
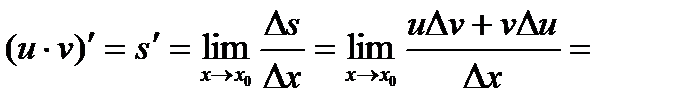

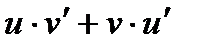 .
.
46. Каково уравнение касательной к графику функции?
Уравнение касательной к графику функции y = f(x) в точке х0 имеет вид 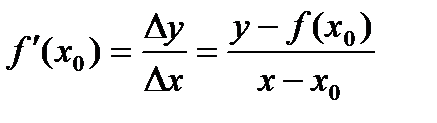 . После преобразований: у = f′(х0)(х – х0) + f(х0). Краткая форма
. После преобразований: у = f′(х0)(х – х0) + f(х0). Краткая форма  более удобна для запоминания.
более удобна для запоминания.
47. Как провести приближённые вычисления функции?
Для этого нужно заменить функцию касательной. Например, для извлечения корня квадратного рассматривается функция 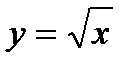 . Её производная равна
. Её производная равна 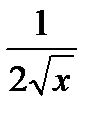 . Пусть требуется извлечь корень из 5 (х = 5), тогда на роль х0 берём близкий к 5 квадрат, например, х0 = 4. Тогда
. Пусть требуется извлечь корень из 5 (х = 5), тогда на роль х0 берём близкий к 5 квадрат, например, х0 = 4. Тогда 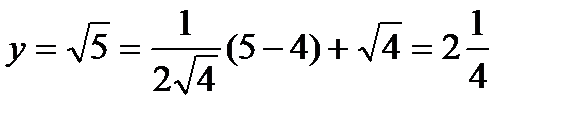 . Для уточнения результата на роль х0 можно взять квадрат полученного значения, то есть (
. Для уточнения результата на роль х0 можно взять квадрат полученного значения, то есть (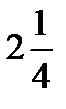 )2.
)2.
48. Что такое нормаль?
Нормаль – это прямая, проходящая через точку касания, и перпендикулярная касательной.
49. Каково уравнение нормали к графику функции?
Уравнение нормали к графику функции y = f(x) в точке х0 имеет вид  . Это связано с тем, что
. Это связано с тем, что 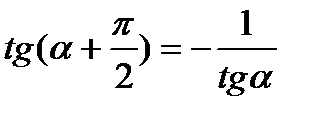 .
.
50. Что такое многочлен?
Многочленом n-й степени называется функция вида у = аn∙xn + аn–1∙xn–1 + … + а1∙x + a0.
51. Что такое корень многочлена?
Пусть задана функция y = f(x). Её корнями называются все решения уравнения f(x) = 0. Таким образом, число х0 является корнем многочлена, если аn∙x0n + аn–1∙x0n–1 + … + а1∙x0 + a0 = 0.
52. Сколько корней может иметь многочлен?
Любой многочлен n-й степени с действительными коэффициентами имеет ровно n комплексных корней. (В этом состоит так называемая основная теорема алгебры). Если же речь идёт о действительных корнях, то многочлен n-й степени имеет не более n действительных корней, в том числе может их не иметь вообще. Например, многочлен у = х2 + 1 действительных корней не имеет.
53. В чём отличие многочленов от других функций?
Отличие и преимущество многочленов перед многими другими видами функций состоит в том, что для их вычисления требуется выполнение только стандартных арифметических операций. Тем же свойством обладают и рациональные функции, которые представляют собой отношение двух многочленов.
54. Любая ли функция является многочленом?
Функция у = sin x имеет бесконечно много корней, следовательно, не может быть многочленом.
55. Какое представление функции является максимально близким к многочлену?
Представление функции в виде бесконечного степенного ряда.
56. Что такое ряд Тейлора?
Ряд Тейлора представляет собой разложение функции в виде f(x) = a0 + а1∙x + а2∙x2 + … + аn–1∙xn–1 + аn∙xn + …. (Часто используется разложение более общего вида: f(x – х0) = a0 + а1∙(x – х0) + а2∙(x – х0)2 + … + аn–1∙(x – х0)n–1 + аn∙(x – х0)n + ….).
57. Каков принцип вычисления коэффициентов ряда Тейлора?
При подстановке х = 0 в ряд Тейлора или же в его производные все члены кроме одного обнуляются, в результате чего один из коэффициент выражается через производную функции f(x).
58. Чему равен n-й коэффициент ряда Тейлора?
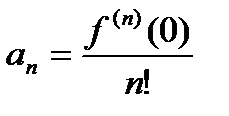 , где n! = 1∙2∙3∙ …∙n, и, кроме того, 0! = 1! = 1.
, где n! = 1∙2∙3∙ …∙n, и, кроме того, 0! = 1! = 1.
59. Для чего нужны ряды Тейлора?
Ряды Тейлора используются для вычисления значений функций.
60. Как вычислить приближённое значение числа е?
Поскольку 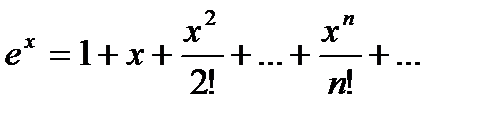 ,
,  .
.
61. Как выглядит простейшее дифференциальное уравнение?
Простейшее дифференциальное уравнение имеет вид y′ = f(x).
62. Какую функцию нужно найти, чтобы решить простейшее дифференциальное уравнение?
Нужно найти такую функцию F(x), производная которой равна f(x).
63. Что такое первообразная?
Пусть задана функции f(x), тогда функция F(x) называется её первообразной, если F′(x) = f(x). Первообразная является решением простейшего дифференциального уравнения y′ = f(x).
64. Как связаны между собой две первообразные одной функции?
Допустим, что функция f(x) имеет две первообразных F1(x) и F2(x). Тогда F′1(x) = f(x) и F′2(x) = f(x). Из этого следует, что F′1(x) – F′2(x) = (F1(x) – F2(x))′ = 0. Поскольку производная функции F1(x) – F2(x) равна нулю, сама эта функция постоянна, то есть F1(x) – F2(x) = С. Таким образом, две любые первообразные одной и той же функции отличаются на постоянную величину.
65. Что такое криволинейная трапеция?
Криволинейная трапеция – это плоская фигура, ограниченная сверху графиком функции f(x), снизу – осью абсцисс, слева – прямой у = а и, наконец, справа – прямой у = b.
66. Что такое площадь?
Площадь фигуры равна числу единичных квадратов, на которую можно разбить фигуру. Однако даже прямоугольник, стороны которого имеют дробную или иррациональную длину, разбить на единичные квадраты нельзя. По этой причине прямоугольник приходится разбивать на квадратики со сторонами, имеющими длину 1/n, суммировать их площади и переходить к пределу. В итоге получается известный результат: площадь прямоугольника равна произведению длин его сторон. Благодаря этому вычисление площадей сложной формы можно провести, разбивая их на прямоугольники и переходя к пределу.
67. Как приближённо вычислить площадь криволинейной трапеции?
| a b |
68. Как найти точное значение площади криволинейной трапеции?
Нужно найти предел суммы слагаемых вида f(x)∆х при ∆х стремящемся к нулю.
69. Что такое определённый интеграл?
Определённым интегралом 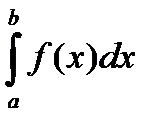 называется предел суммы слагаемых вида f(x)∆х при ∆х стремящемся к нулю.
называется предел суммы слагаемых вида f(x)∆х при ∆х стремящемся к нулю.
70. Каков геометрический смысл определённого интеграла?
| a х х+∆х |
71. Как получить функцию, используя определённый интеграл?
Определённый интеграл является числом. Однако с его помощью можно построить функцию. Рассмотрим площадь S(x) криволинейной трапеции на отрезке [a; х]. Она равна  (буква ξ использована, чтобы не перегружать переменную х) При изменении левого конца отрезка меняется площадь S(x), а это означает, что величина S(x) является функцией, зависящей от х.
(буква ξ использована, чтобы не перегружать переменную х) При изменении левого конца отрезка меняется площадь S(x), а это означает, что величина S(x) является функцией, зависящей от х.
72. Чему равна производная площади криволинейной трапеции с переменным пределом интегрирования?
Придадим аргументу приращение ∆х. Тогда исходная трапеция увеличится за счёт полоски шириной ∆х. Приблизительно её площадь равна f(x)∆x, а это означает, что ∆S = f(x)∆x. Таким образом,  .
.
73. Что такое неопределённый интеграл?
С помощью определённого интеграла удалось построить функцию, которая является первообразной для функции f(x), находящейся под знаком интеграла. По этой причине первообразную называют неопределённым интегралом и обозначают через 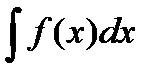 .
.
74. Чем отличаются определённый и неопределённый интеграл?
Определённый интеграл – это число, а неопределённый интеграл – это функция.
75. Какой вид имеет формула Ньютона – Лейбница?
Пусть нам даны функция f(x) и её первообразная F(x), тогда 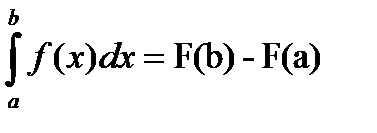 . Формула Ньютона – Лейбница помогает вычислять определённые интегралы в случаях, когда известна первообразная функции, находящейся под знаком интеграла.
. Формула Ньютона – Лейбница помогает вычислять определённые интегралы в случаях, когда известна первообразная функции, находящейся под знаком интеграла.
76. Как практически вычислить площадь криволинейной трапеции?
Зная первообразную функции, ограничивающей криволинейную трапецию, легко вычислить площадь с помощью формулы Ньютона – Лейбница. Например, площадь арки синусоиды равна 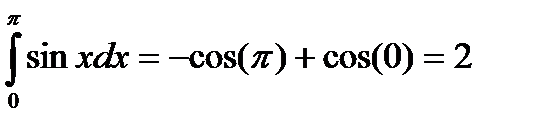 .
.
77. Каковы основные способы интегрирования?
Прежде всего, следует проверить, не является ли интеграл табличным. Табличными интегралами называются те интегралы, которые непосредственно получаются из формул дифференцирования элементарных функций. Далее следует проверить применимость методов замены переменной и интегрирования по частям.
78. На чём основан и в чём состоит метод замены переменной?
Метод замены переменной основан на формуле дифференцирования сложной функции  . Формула интегрирования имеет вид
. Формула интегрирования имеет вид  . Метод применяется в тех случаях, когда под интегралом стоит выражение, содержащее некоторую функцию, и это выражение умножено на производную этой функции. Например, вычисляя интеграл
. Метод применяется в тех случаях, когда под интегралом стоит выражение, содержащее некоторую функцию, и это выражение умножено на производную этой функции. Например, вычисляя интеграл 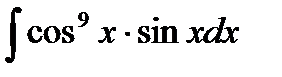 , можно заметить, что под интегралом стоит выражение от cos x, умноженное на sin x, то есть производную косинуса. Делаем замену cos x = u, далее получаем sin x∙dx = du. В итоге
, можно заметить, что под интегралом стоит выражение от cos x, умноженное на sin x, то есть производную косинуса. Делаем замену cos x = u, далее получаем sin x∙dx = du. В итоге 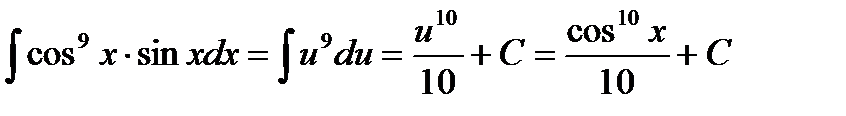 .
.
79. На чём основан и в чём состоит метод интегрирования по частям?
Метод замены переменной основан на формуле дифференцирования произведения двух функции d(uv) = u∙dv + v∙du. Отсюда следует, что u∙dv = d(uv) – v∙du. И наконец 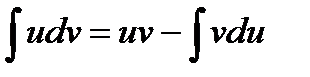 . Метод применяется в тех случаях, когда под интегралом стоит легко интегрируемая функция и функция, упрощающаяся при дифференцировании. Например, вычисляя интеграл
. Метод применяется в тех случаях, когда под интегралом стоит легко интегрируемая функция и функция, упрощающаяся при дифференцировании. Например, вычисляя интеграл  , следует положить, что u = x, dv = exdx, тогда du = dx, v = ex. Окончательно получаем
, следует положить, что u = x, dv = exdx, тогда du = dx, v = ex. Окончательно получаем

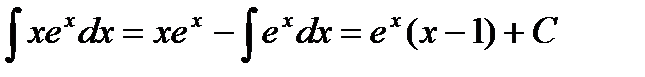 .
.
80. Как использовать определённый интеграл для вычисления объёмов?
Нужно разрезать тело, объём которого вычисляется, на тонкие блинчики толщиной dx и просуммировать их объёмы (проинтегрировать). Например, пусть на отрезке [a; b] задана функция f(x). При её вращении вокруг оси абсцисс возникает тело вращения. Вычислить объём этого тела. Блинчик представляет собой цилиндр радиуса f(x), следовательно, его объём равен π∙f(x)2dx. Объём тела вращения равен π∙  . Вычисления этого интеграла следует проводить для каждой конкретной функции.
. Вычисления этого интеграла следует проводить для каждой конкретной функции.
81. Как использовать определённый интеграл для вычисления длин кривых?
Пусть на отрезке [a; b] задана функция f(x). Чтобы вычислить её длину, разобьём отрезок [a; b] на части длины dx. Функция на этой частичке прирастёт на dy. Длина соответствующего кусочка кривой равна 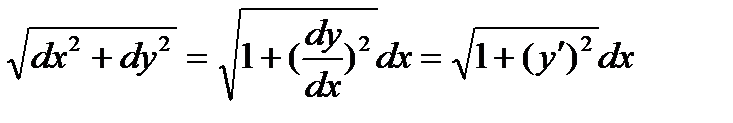 . Длина всей кривой равна
. Длина всей кривой равна 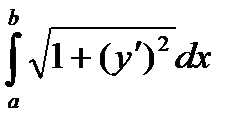 .
.
82. Каковы основные виды элементарных функций?
Линейная функция, степенные функции, многочлены, дробно-рациональные функции (отношения многочленов), тригонометрические функции и обратные к ним, показательные функции и логарифмы.
83. Что представляют собой замечательные пределы?
Замечательные пределы – это пределы, применяющиеся для вычисления производных некоторых важных элементарных функций (синуса, логарифма, показательной функции, степенной функции):
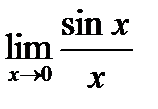
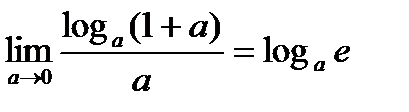
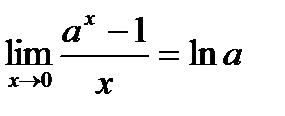
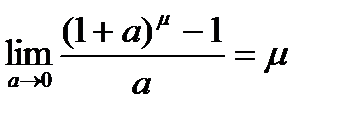
84. В чём состоит правило Лопиталя?
Пусть  при
при 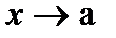 и
и 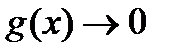 при
при  . Тогда в случае существования производных
. Тогда в случае существования производных  и
и  (
(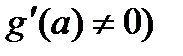 имеем:
имеем: 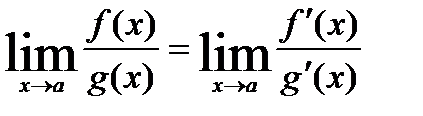 . Действительно,
. Действительно,  . Остается перейти к пределу при
. Остается перейти к пределу при  .
.
85. От любых ли функций, являющихся комбинациями элементарных функций, можно брать производные??
Производные от любых комбинаций элементарных функций могут быть найдены с помощью таблиц производных и основных правил дифференцирования, в том числе дифференцирования сложных функций.
86. От любых ли функций, являющихся комбинациями элементарных функций, можно брать интегралы?
Операция дифференцирования является более сложной, чем операция дифференцирования. Некоторые интегралы не выражаются через элементарные функции. Например, не могут быть выражены через элементарные функции интегральный логарифм 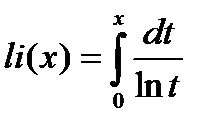 , интегральный синус
, интегральный синус  и интегральный косинус
и интегральный косинус 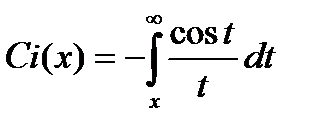 . Все эти выражения относятся к классу специальных функций. Легко интегрируются многочлены. Существуют методы интегрирования дробно-рациональных функций.
. Все эти выражения относятся к классу специальных функций. Легко интегрируются многочлены. Существуют методы интегрирования дробно-рациональных функций.
87. Что такое функция двух переменных?
Функция от двух переменных представляет собой зависимость переменной z от двух независимых переменных х и у. Эта зависимость обозначается через z = F(x,y). Изучение функции от двух переменных естественным образом увязывается с декартовой системой координат в трехмерном пространстве. Роль графика функции z = F(x,y) играет некоторая поверхность, образованная точками с координатами (x, y, F(x,y)). На функции нескольких переменных переносятся такие понятия как область определения, область значений, непрерывность. Функция называется непрерывной, если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.
88. Что такое частная производная?
В случае, если мы зафиксируем один из аргументов функции двух переменных, мы получим функцию одного переменного:  , где
, где 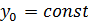 . Допустим, что эта функция дифференцируема в точке
. Допустим, что эта функция дифференцируема в точке 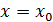 , тогда её производная равна
, тогда её производная равна 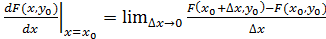 Она называется частной производной по x и обозначается через
Она называется частной производной по x и обозначается через  или
или  . Аналогично вводится и частная производная по y и обозначается через
. Аналогично вводится и частная производная по y и обозначается через 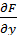 .
.
89. Чему равно полное приращение функции от двух переменных?
Выражение 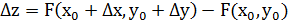 называется полным приращением функции z = F(x, y) в точке (х0; у0). Если частные производные
называется полным приращением функции z = F(x, y) в точке (х0; у0). Если частные производные 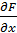 и
и 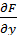 существуют и непрерывны в некоторой окрестности точки
существуют и непрерывны в некоторой окрестности точки  , то имеет место формула
, то имеет место формула  , где
, где 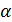 и
и  зависят от
зависят от  и
и  и вместе с ними стремятся к нулю. Полным дифференциалом функции двух переменных называется линейная часть приращения функции:
и вместе с ними стремятся к нулю. Полным дифференциалом функции двух переменных называется линейная часть приращения функции: 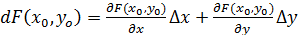 .
.
90. Каково уравнение касательной плоскости к поверхности, описываемой функцией от двух переменных?
Уравнение касательной плоскости к поверхности имеет вид 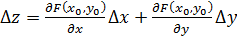 или
или 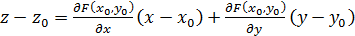 .
.
91. Что такое неявная функция?
Пусть F(x, y) функция двух переменных, выражение F(x, y) = 0 можно рассматривать как определение функции y = f(x) такой, что F(x, f(x)) = 0.






