Изменение вторичного напряжения трансформатора при нагрузке и его внешние характеристики

Лекция 19

Реальный трансформатор

 

При детальном исследовании процессов, наблюдаемых в реальных трансформаторах (рис. 11.4), необходимо учитывать магнитные поля рассеяния и активные сопротивления обмоток трансформатора. На рис. 11.4 изображены магнитные линии полей рассеяния первичной Ф_σ1 и вторичной Ф_σ2 обмоток. Магнитные линии каждого из этих магнит­ных потоков рассеяния сцеплены только с витками своей обмотки, т. е. эти магнитные потоки не участвуют в передаче энергии из первичной цепи во вторичную. Однако в каждой из обмоток они наводят э. д. с. соответственно

 (11.25)

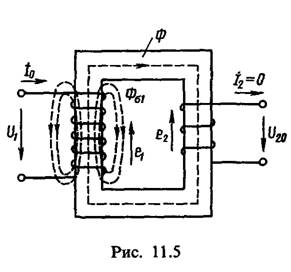Режим холостого хода трансформатора. При режиме холостого хода первичная обмотка трансформатора подключена к электрической сети, а от вторичной обмотки отключена нагрузка (рис. 11.5). Режим холостого хода ничем не отличается от работы катушки с ферромаг­нитным сердечником, рассмотренной в гл. 8, поэтому все соотношения и векторная диаграмма справедливы для случая холостого хода трансфор­матора.

 

В реальном трансформаторе ток холостого хода I₀ наряду с реактивной составляющей тока I_0р, создающей в магнитопроводе трансформатора основной поток Ф, имеет также и активную состав­ляющую I_оa, которая обусловлена потерями энергии на гистерезис и вихревые токи в магнитопроводе. Поэтому ток холостого хода

 (11.26)

Следует отметить, что в трансформаторах при выполнении магнито-провода из листов электротехнической стали толщиной 0,35—0,5 мм и частоте 50 Гц активная составляющая тока холостого хода не пре­вышает 10 % от I₀, вследствие чего I_0а не оказывает заметного влияния на значение тока холостого хода.

При прохождении тока I₀ кроме основного магнитного потока Ф в магнитопроводе первичной обмотки наводится поток рассеяния Ф_σ1.

Поток Ф_σ1 индуцирует в первичной обмотке трансформатора э. д. с. рассеяния E_σ1. Так как поток рассеяния Ф_σ1 замыкается в основном по воздуху, то он пропорционален м. д. с. первичной обмотки или первич­ному току, поэтому E_σ1 = I₀Х₁, где Х₁ — индуктивное сопротивление первичной обмотки трансформатора, обусловленное потоком рассеяния Ф_σ1. Так как вектор Е_σ1 отстает от потока и тока на угол π/2, то для э. д. с. можно записать

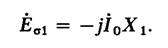 (11.27)

В реальном трансформаторе первичная обмотка обладает активным сопротивлением r₁, на котором при прохождении тока I₀ имеется падение напряжения I₀r₁,  поэтому, согласно второму закону Кирхгофа, уравнение трансформатора для первичной цепи при холостом ходе имеет вид

                        (11.28)

откуда

где Z ₁ = r₁ + jX₁ — комплекс­ное значение полного сопротив­ления первичной обмотки трансформатора;  — модуль полного сопротивления первичной обмотки трансфор­матора.

На основании уравнений (11.26) и (11.29) можно построить векторную диаграмму (рис. 11.6, а) и схему замещения (рис. 11.6,б) реального транс­форматора в режиме холостого хода.

 

 Построение векторной диаграммы удобно начать с максимального вектора основного потока Ф _m. Если основной магнитный поток изменяется по синусоидальному закону, то и наводимые им э. д. с. E₁ и E ₂ отстают от потока Ф _m на угол π/2. Построение вектора тока холостого хода I₀ производят из точки O согласно уравнению (11.26), причем реактивная составляющая I _{0 p} сов­падает по направлению с создаваемым ею потоком Ф _m),  а активная составляющая I _оа опережает поток Ф _m на угол π/2. Вектор тока I ₀ опе­режает вектор магнитного потока Ф _m на угол α, который зависит от потерь в ферромагнитном сердечнике трансформатора на гистерезис и вихревые токи, т. е. от так называемых потерь в стали. Практически угол α = 5^o - 10°.

Вектор потока рассеяния первичной обмотки Ф_σ1 откладывают из точки О в направлении тока I ₀, а вектор индуцируемой этим потоком рассеяния э. д. с. E _σ1 отстает от него на угол π/2.

Согласно уравнению (11.29), из точки О строят вектор приложенно­го напряжения U₁, который представляет собой сумму трех векторов.

В реальных силовых трансформаторах, за исключением самых мало­мощных, падение напряжения в первичной обмотке I₁Z₁ при полной нагрузке составляет несколько процентов от первичного напряжения U₁. Так как ток холостого хода I₀ для трансформаторов [за исклю­чением маломощных (до 1 кВА)] составляет 3% — 10% от номиналь­ного первичного тока I₁,  то значение падения напряжения в первич­ной обмотке при холостом ходе IoZ₁ очень мало и составляет десятые доли процента от U₁. Поэтому первичное напряжение U₁ при холостом ходе трансформатора практически можно считать равным э. д. с. E₁,  но противоположным ей по фазе [см. (11.30)]. Во вторичной же обмотке при холостом ходе из-за отсутствия в ней тока U₂₀ = E₂.

Следовательно, при холостом ходе первичное и вторичное напряже­ния практически равны по значению соответствующим э. д. с. и коэф­фициент трансформации можно с достаточной степенью точности опре­делить как отношение напряжений на зажимах обмоток трансформа­тора при холостом ходе:

 (11.31)

Величину – E₁ в уравнении (11.30) можно представить в виде произведения тока холостого хода и сопротивления контура намагничивания Z _m: - E ₁ = I ₀ Z _m.

Так как ток I ₀ отстает по фазе от напряжения – E ₁,  то сопротивление Z _m должно иметь как активную r_m,  так и индуктивную Х_m составляющие: Z _m = r_m +jХ_m. Учитывая это, уравнение (11.30) можно записать в виде

Согласно уравнению (11.32), схему замещения трансформатора можно представить в виде, показанном на рис. 11.6, б. Участок схемы замеще­ния, находящийся между точками а и b, через который проходит ток I₀, называют намагничивающим контуром. Энергия, выделяемая на этом участке в сопротивлениях Х_m и r_m, затрачивается на создание основного магнитного потока в магнитопроводе трансформатора и на компенсацию активных потерь, возникающих в магнитопроводе за счет гистерезиса и вихревых токов.

Входное сопротивление трансформатора при холостом ходе является суммой сопротивлений  Мощность, потребляемая трансформатором из электрической сети при холостом ходе, затрачивается на компенсацию потерь в магнитопроводе и в про­водниках первичной обмотки I₀²r₁ (электрические потери).

Если электрические потери I₁²r_l в первичной обмотке и I₂²r₂ во вто- ричной обмотке нагруженного трансформатора составляют 3% — 0,5% от его номинальной мощности (с ростом мощности трансформатора эти потери снижаются в процентном отношении), то при холостом ходе из-за того, что ток I₀ невелик и сопротивление r₁ сравнительно мало, электрические потери по сравнению с потерями в стали оказываются небольшими. Исключением являются маломощные трансформаторы с номинальной мощностью ниже 100 ВА. Таким образом, мощность, потребляемая из сети трансформатором при холостом ходе, практически полностью затрачивается на покрытие потерь в стали. Следовательно, на основании испытания трансформатора при разомкнутой цепи вто­ричной обмотки и номинальном первичном напряжении U_lx = U_1н (так называемого опыта холостого хода) можно определить потери в стали трансформатора.

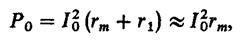Измерив мощность Р₀, потребляемую трансформатором при холостом ходе, и ток холостого хода I₀, можно найти параметры кон­тура намагничивания: r_m, X_m, Z _m. Так как при холостом ходе электри­ческими потерями в первичной обмотке трансформатора I₀²r₁ обычно пренебрегают и вся мощность, потребляемая трансформатором из электросети, расходуется на компенсацию потерь в стали, то в уравне­нии (11.32) можно принять, что r_m + r₁ ≈ r_m и  X_m + X₁ ≈ X_m (так как r_m >> r₁ и Х_m >> X₁, например, потому, что сопротивление Х_m опреде­ляется основным потоком трансформатора Ф, а Х₁ — потоком рассеяния Ф_σ1, который во много paз  меньше Ф). Следовательно, мощность, потребляемая трансформатором при холостом ходе,

откуда

 (11.33)

Считая    находим

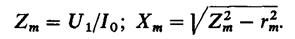 (11.34)

Рабочий режим трансформатора. Рассмотрим процессы, протекаю­щие в трансформаторе в рабочем режиме, когда учитываются магнитное поле рассеяния и активное сопротивление первичной и вторичной об­моток трансформатора. В нагруженном трансформаторе (см. рис. 11.4) наряду с основным магнитным потоком Ф, индуцирующим э. д. с. E₁ в первичной и E₂ во вторичной обмотках, потоки рассеяния Ф_σ1 и Ф_σ2 индуцируют в первичной и вторичной обмотках э. д. с. рассея­ния Е_σ1 = - jI₁X_i, E_σ2 = - jI₂X₂,  где X₁ и Х₂ — индуктивные сопротив­ления, обусловленные потоками Ф_σ1 и Ф_σ2. С учетом падений напряжений в активных сопротивлениях обмоток всех э. д. с., наводимых в них согласно второму закону Кирхгофа, запишем уравнения электри­ческого состояния для первичной и вторичной цепей в комплекс­ной форме:

где Z _H = r_н + j X_н — сопротивление активно-индуктивной нагрузки, мо­дуль которого  ; I₂Z_Н = U₂ — падение напряжения в на­грузке, которое равно вторичному напряжению трансформатора. При замене э. д. с. E_σ1и E_σ2 падениями напряжений  - jI₁X₁ и  - jI₂Х₂   урав­нения (11.35) и (11.36) примут вид

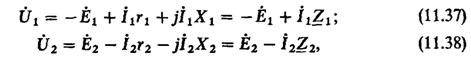
где Z ₁ = r₁ + jX₁  — сопротивление первичной обмотки трансформа­тора, модуль которого  ; Z ₂ = r₂ + jХ₂ — сопротивление вторичной обмотки трансформатора, модуль которого .

Замена э. д. с. рассеяния падениями напряжений возможна потому, что потоки рассеяния обмоток трансформатора создают индуктивные падения напряжения в обмотках и не участвуют в передаче энергии из первичной обмотки во вторичную.

На практике у трансформаторов магнитные потоки рассеяния Ф_σ1 и Ф_σ2 в десятки раз меньше основного потока Ф и падения напряже­ний I₁r₁ и I₂r₂ обмоток также малы, поэтому для реального трансфор­матора первичное напряжение U₁ в основном уравновешивается э. д. с. E₁  (U ₁ ≈ - E ₁). Следовательно, для реального нагруженного трансформа­тора справедливо уравнение магнитодвижущих сил, полученное для идеализированного трансформатора:

 (11.39)

Из (11.39) следует, что м. д. с. первичной обмотки компенсирует размагничивающее действие м. д. с. вторичной обмотки и поддержи­вает неизменным основной поток в магнитопроводе трансформатора.

Уравнение м. д. с. (11.39) преобразуют в уравнение токов:

 (11.40)

Так как ток холостого хода I₀составляет не более 10 % от первичного тока I₁, то значительная часть тока I₁ идет на компенсацию размагни­чивающего действия вторичного тока.

Уравнения (11.37), (11.38) и (11.40) позволяют построить векторную диаграмму нагруженного трансформатора, для чего необходимо знать параметры трансформатора r₁ г₂, Х₁ Х₂, I₀,коэффициент трансформа­ции k, угол потерь α, а также параметры нагрузки, т. е. ток I₂,напряже­ние U ₂ исоsφ₂,  характер нагрузки также должен быть известен. На рис. 11.7 изображена векторная диаграмма при активно-индуктивном характере нагрузки.

Векторную диаграмму для вторичной цепи трансформатора строят согласно уравнению (11.38). Ее построение начинают с вектора амплитуд­ного значения основного магнитного потока Ф _m или с вектора напря­жения U ₂. Начнем построение с вектора Ф _m, расположив его от точки О горизонтально. Затем строим векторы э. д. с. E ₁ и E ₂, которые отстают от потока Ф _m на угол π/2. При активно-индуктивном характере нагрузки Z _H = r_н+ jХ_н,а вектор тока I ₂ необходимо откладывать под углом ψ₂ = arctg (Х₂ + X_H)/(r₂ + r_Н) в сторону отставания от векторов E₂ и E ₁. Вектор I ₂ r ₂ откладывают параллельно вектору тока I ₂, а вектор jI ₂ X ₂ — под углом π/2 в сторону опережения вектора I ₂.

Векторы I ₂ r ₂ и jI ₂ X ₂ - катеты треугольника внутренних падений напряжений вторичной обмотки, гипотенузой которого является вектор I ₂ Z ₂. Падения напряжения в сопротивлении нагрузки U ₂ и в сопротивлении вторичной обмотки I ₂ Z ₂ уравновешивают э. д. с. E ₂.

Векторную диаграмму первичной цепи трансформатора строят ана­логичным образом. Вначале откладывают вектор тока I ₀, который опережает вектор потока Ф _m на угол потерь α. После этого, зная направление вектора I ₂, можно построить вектор – I ₂ w ₂ / w ₁, а затем и вектор I ₁, как сумму векторов I ₀ и – I ₂ w ₂ / w ₁. Затем, зная длину и направ­ление вектора тока I ₁, определяют значения и направления векторов I ₁ r ₁ и jI ₁ X ₁ и строят искомый вектор U ₁ как сумму трех составляю­щих: вектора - E ₁ и векторов падений напряжений в первичной обмотке I ₁ r ₁ и jI ₁ X ₁.

Следует отметить, что на векторной диаграмме для наглядности длины векторов падений напряжений в обмотках трансформатора и тока холостого хода выбраны существенно большими, чем они есть в реаль­ном трансформаторе. В частности, падения напряжений в обмотках обычно составляют лишь несколько процентов от э. д. с. E₁ и E₂.

Из векторной диаграммы рис. 11.7 видно, что при активно-индуктивном характере на­грузки напряжение U ₂ меньше э. д. с. Е₂ и что с увеличением тока нагрузки I ₂ напряжение U₂на зажимах вторичной обмотки уменьшается. Изменение тока нагрузки I₂сопровождается автоматическим изменением тока I₁ первичной цепи трансформатора. Эту взаимосвязь можно объяснить с помощью уравнения равновесия м. д. с. (I_ow ₁ = I ₁ w ₁ + I ₂ w ₂)или уравнения токов (I о = I ₁ – w ₂ I ₂ / w ₁ = I ₂ + I ₂ ^’ ).Так как при напряжении сети U₁ = const результирующая м. д. с. при различных нагрузках практически остается неизменной (I₀w₁ =.const или I₀ = const), то при изменении вторичного тока на ΔI₂ происходит изменение первичного тока на ΔI₁ = ΔI₂^’. Это утверждение спра ведливо для нагрузок, при которых токи в обмотках транс­форматора не превышают номинальных значений: при изменении нагрузки трансформатора без превышения его номинальной мощности рабочий магнитный поток в магнитопроводе трансформатора остается неизменным, а значит, неизменной оказывается и результирующая м. д. с.

Схема замещения реального трансформатора. Реальный трансформа­тор отличается от идеализированного тем, что в нем учитываются активные r₁и r ₂ и индуктивные Х₁и Х₂сопротивления, соответствую­щие первичной и вторичной обмоткам. Учитывая это и используя метод приведения величин вторичной цепи трансформатора к первичным, можно построить схему замещения для реального нагруженного трансформатора, в которой электромагнитная связь между обмотками заменена электрической связью (рис. 11.8). На схеме замещения при­веденное активное сопротивление вторичной обмотки определяют из условия, по которому потери в ней при приведении остаются неизмен­ными, т. е.

 (11.41)

Используя выражения (11.19) л (11.41), находим

 (11.42)

Приведенное индуктивное сопротивление вторичной обмотки определяют из условия неизменного фазового сдвига между током и напряжением в этой обмотке:

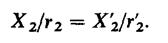 (11.43)

Используя выражения (11.42) и (11.43), получим

 (11.44)

На схеме замещения для нагруженного рансформатора рис. 11.8 кроме приведенных величинr'₂, Х'₂, r'_н, Х'_нпоказано также приведенное напряжение нагрузки U'₂, которое определяется той же формулой, что и при построении схемы замещения идеализированного трансформа­тора, т. е.

Режим короткого замыкания трансформатора. Режим короткого замыкания трансформатора (вторичная обмотка замкнута накоротко, Z_H = 0) в эксплуатационных ус­ловиях является аварийным, так как токи во вторичной обмотке превышают в 7 — 20 раз номи­нальные. По­этому опыт короткого замы­ кания для экспериментального  определения параметров трансформатора может быть осуществлен при сильно пониженном напряжении первичной обмотки. При опыте короткого замыкания напряжение источника питания понижают с помощью регулятора напряжения до значения U_1к. Это напряжение должно быть таким, чтобы в обмотках трансформатора проходили номинальные токи I₁ и I₂, и называется напряжением короткого замыкания. Оно выражается в процентах от номинального значения:

 (11.45)

Напряжение U_kсоставляет обычно 5—15% от номинального значе­ния и тем больше, чем выше номинальные напряжение и мощность трансформатора.

Рабочий магнитный поток Ф, замыкающийся через ферромагнитный сердечник трансформатора, зависит от приложенного к первичной обмотке напряжения, а магнитные потери в стали пропорциональны квадрату магнитного потока Ф². Поэтому при опыте короткого замы­кания, ввиду того что приложенное напряжение короткого замыкания Uк невелико, магнитный поток в магнитопроводе трансформатора весьма мал и можно считать, что I₀ ≈ 0. Таким образом, при опыте короткого замыкания потерями в стали и током холостого хода I₀ можно пренебречь. На этом основании можно считать, что вся мощ­ность, потребляемая трансформатором при опыте короткого замы­кания, расходуется на покрытие электрических потерь в проводниках обмоток:

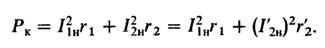 (11.46)

Так как при опыте короткого замыкания ток I₀ ≈ 0, то м. д. с. первичной обмотки будет компенсировать м. д. с. вторичной обмотки и уравнение магнитного равновесия можно записать в следующем виде:

 (11.47)

Так как при I₀=0 токи I₁ и I₂ находятся в противофазе, то геометрическое суммирование можно заменить алгебраическим I₁w₁ + I₂w₂ = 0, откуда I₁ = - w₂I₂/w₁, и выражение (11.46) можно переписать в виде

 (11.48)

В этом случае из общей схемы замещения трансформатора исклю­чают контур намагничивания с сопротивлениями r_mи Х_mи преобра­зуют ее в схему, представленную на рис. 11.9, a. Параметры схемы замещения трансформатора при опыте короткого замыкания определяют с помощью следующих соотношений:

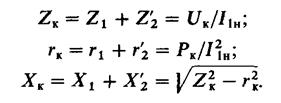 (11.49)

На рис. 11.9,б представлена векторная диаграмма, соответствую­щая упрощенной схеме замещения приведенного трансформатора при

режиме короткого замыкания. Треугольник ОВС на этой диаграмме называется треугольником короткого замыкания или характеристиче­ ским треугольником. Его катеты ОС и ВС. называют соответственно активной и реактивной составляющими напряжения короткого замы­кания.

В паспорте каждого трансформатора указывают относительное значение напряжения короткого замыкания U_K при номинальном токе в процентах от номинального напряжения. По данным опыта корот­кого замыкания определяют относительные значения активной U_ka и реактивной U_kp, составляющих напряжения короткого замыкания, а также и само напряжение U_k, %:

Напряжение короткого замыкания является величиной, важной для практики, так как она позволяет определить изменение вторичного напряжения трансформатора при нагрузке.

 

Изменение вторичного напряжения трансформатора при нагрузке и его внешние характеристики

 

При переходе от режима холостого хода к режиму работы под нагрузкой вторичное напряжение трансформатора изменяется. При по­стоянном значении первичного напряжения U_l = U_1н= const разность между вторичными напряжениями в этих режимах называется процент­ ным изменением вторичного напряжения трансформатора и равна:

Так как при холостом ходе падение напряжения в обмотках трансфор­матора отсутствует, то U₁ = U'₂₀и тогда при номинальном значении первичного напряжения U₁ = U_1н

 (11.54)

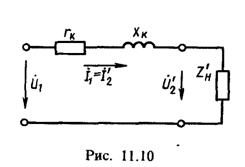
На рис. 11.10,б представлена векторная диаграмма, построенная согласно упрощенной схеме замещения (рис. 11.10, а). С помощью этой диаграммы можно найти изменение вторичного напряжения трансформа­тора при нагрузке. В самом деле, из-за небольшого сдвига фаз между U_1н и U'₂ (φ₁ – φ₂ = 3 - 5°) за модуль вектора U_1н можно принять его проекцию (отрезок ОС) на направление вектора U'₂ (рис. 11.10,б). Разность между этой проекцией и вектором U'₂(отрезок ОА) равна изменению напряжения Δu = U₁ - U'₂ = ОС - ОА = АС. Затем, спрое­цировав векторы I ₁ r_k и jI ₁ X_k на направление вектора U'₂, имеем

Тогда процентное изменение вторичного напряжения

 (11.55)

Из этого уравнения следует, что изменение вторичного напряжения пропорционально току нагрузки: I'₂ ≈ I₁. Вводя коэффициент нагрузки

β = I₂I_2н ≈ I₁/I_1н, можно получить

 (11.56)

т. е. изменение вторичного напряжения пропорционально коэффициенту нагрузки β.

Внешней характеристикой трансформатора называют зависимость вторичного напряжения U₂от тока нагрузки I ₂ при U₁ = U_lн = const,      cos φ₂ = const и f = f_н= const. Для построения внешних характеристик используют полученное согласно (11.54) и (11.56) уравнение

 (11.57)

Из рис. 11.11 видно, что внешние характеристики трансформатора практически прямолинейны, если коэффициент нагрузки находится в пре-

делах от 0 до 1. Кривая 1 соответствует чисто активной нагрузке (Z_Н = r_Н)  и cosφ ₂ = 1,  кривая 2 -активно-индуктивной нагрузке (Z _Н = r_Н + jX_Н),  cos φ₂ = 0,8 при φ₂ > 0, а кривая 3— активно-емкостной нагрузке (Z _Н = r_Н -  jX_H ) и cos φ₂ = 0,8 при φ₂ < 0. При 0 < β < 1 напряжение на зажимах вторичной обмотки трансформатора изменяется лишь на несколько процентов, обеспечивая практически стабильное напряжение.