Главная Побочная
Образец выполнения работы № 2
Задача №1
Пример 1
Найти минимальный среди нечетных элементов под главной диагональю матрицы произвольного размера одинаковой длины.
Решение
Sub Zadanie_1()
Const N=6 ‘ Размерность матрицы
Dim A(N,N) as Integer, I as Integer, J as Integer
Dim Min as Integer, Imin as Integer, Jmin as Integer
Randomize
For I=1 To N
For J=1 To N
A(I,J) = Int(Rnd*10 – 5) ‘ Формирование матрицы
Cells(I,J) = A(I,J) ‘ случайным образом
Next J,I
Min = 32000
For I=1 To N
For J=1 To N
If (A(I,J)<=Min) And (A(I,J) Mod 2<>0) And (I>J) Then ‘ Поиск
Min = A(I,J) ‘ минимума и его
Imin = I ‘ номера строки и
Jmin = J ‘ номера столбца
End If
Next J,I
Cells(N+2,1) = “Min =” ‘ Вывод результатов
Cells(N+2,2) = Min
Cells(N+3,1) = “IMin =”
Cells(N+3,2) = IMin
Cells(N+4,1) = “JMin =”
Cells(N+4,2) = JMin
End Sub
Пример 2
Определить количество нулевых элементов в каждом столбце матрицы произвольного размера.
Решение
Sub Zadanie_1a()
Const N=6, M=5 ‘ Размерность матрицы
Dim A(N,M) as Integer, I as Integer, J as Integer
Dim K as Integer
For I=1 To N
For J=1 To M
A(I,J) = Int(Rnd*10 – 5)
Cells(I,J) = A(I,J)
Next J,I
For J=1 To M ‘ Цикл по столбцам
K = 0 ‘ Начальное значение
For I=1 To N ‘ Цикл по строкам
If A(I,J) = 0 Then K = K+1 ‘ Поиск количества
Next I ‘ Конец цикла по строкам
Cells(N+2,J) = “K =” & K ‘ Вывод результата в J столбец
Next J ‘ Конец цикла по столбцам
End Sub
Задача №2
Сформировать матрицу B(8,9) следующего вида:
4 5 5 5 5 5 5 5 1
4 0 5 5 5 5 5 2 2
4 0 0 5 5 5 3 3 3
4 0 0 0 5 4 4 4 4
4 0 0 0 5 5 5 5 5
4 0 0 6 6 6 6 6 6
4 0 7 7 7 7 7 7 7
4 8 8 8 8 8 8 8 8
Решение
Sub Zadanie_2()
Const N = 8, M = 9
Dim B(8,9) as Integer, I as Integer, J as Integer
WorkSheets(“Лист2”).Select
For I=1 To N
For J=1 To M
If I+J>M+1 Then B(I,J) = I ‘ Область под побочной диагональю
If (I<J) And (I+J < M+1) Then B(I,J) = 5 ‘ Верхний треугольник – цифра 5
If J = 1 Then B(I,J) = 4 ‘ Первый столбец – цифра 4
Cells(I,J) = B(I,J)
Next J,I
End Sub
Задача №3
Вычислить все значения функции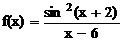 
на промежутке от –3 до 5 с шагом h=0,3 с использованием подпрограммы.
Решение
Function f(x as Single) as Single ‘ Подпрограмма-функция
f = (Sin(x+2))^2/(x-6) ‘ вычисления функции
End Function
Sub Zadanie_3()
Dim x as Single, Y as Single
WorkSheets(“Лист3”).Select ‘ Выбор 3-го листа
Cells(1,1) = “X” ‘ Печать заголовков
Cells(1,2) = “Y” ‘ в первой строке
I = 2 ‘ Номер строки для вывода –2
For x = -3 To 5 Step 0.3
Y = f(x) ‘ Вызов функции
Cells(I,1) = x ‘ Вывод значения x
Cells(I,2) = Y ‘ Вывод значения Y
I = I + 1 ‘ Номер строки - следующий
Next x
End Su
Практическая часть
Задание № 1
 Последняя цифра номера зачетной книжки
| Начало текста |
| 0 | Определить сумму и количество элементов, больших 6, по абсолютной величине |
| 1 | Определить сумму и произведение отрицательных четных элементов |
| 2 | Определить минимальный элемент и его местоположение (№ строки и столбца) среди нечетных положительных элементов |
| 3 | Определить максимальный элемент среди отрицательных и его местоположение (№ строки и столбца) |
| 4 | Определить среднее арифметическое всех положительных элементов, кратных 5 |
| 5 | Определить произведение и количество четных элементов, больших 7 |
| 6 | Определить минимальный элемент и его местоположение (№ строки и столбца) среди четных отрицательных элементов |
| 7 | Определить сумму и количество элементов, попадающих в интервал (0;5) |
| 8 | Определить максимальный элемент и его местоположение (№ строки и столбца) среди элементов, кратных 3 |
| 9 | Определить произведение и количество элементов, больших 3 |
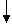 Предпоследняя цифра номера зачетной книжки
| Окончание текста |
| 0 | В первом столбце матрицы произвольного размера |
| 1 | В последних трех столбцах матрицы произвольного размера |
| 2 | В каждой строке квадратной матрицы |
| 3 | В четных столбцах матрицы произвольного размера |
| 4 | В нечетных строках матрицы произвольного размера |
| 5 | В каждом столбце матрицы произвольного размера |
| 6 | Во второй и третьей строках матрицы произвольного размера |
| 7 | На главной диагонали квадратной матрицы |
| 8 | Над побочной диагональю квадратной матрицы |
| 9 | В первых трех строках матрицы произвольного размера |
Задание № 2
Сформировать матрицу:
Имя[размер] (вариант – последние две цифры номера зачетной книжки)
| А[7 x 7] (01, 21, 41, …, 81) | В [7 x 7] (02, 22, 42, …, 82) |
| 
|
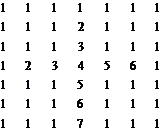
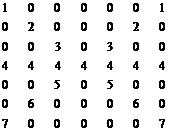
| С [7 x 8] (03, 23, 43, …, 83) | D [8 x 8] (04, 24, 44, …, 84) |
| 
|
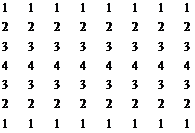
| E [5x9] (05, 25, 45, …, 85) | F [5x5] (06, 26, 46, …, 86) |
| 
|
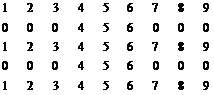
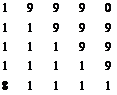
| G [5x5] (07, 27, 47, …, 87) | H [5x9] (08, 28, 48, …, 88) |
| 
|
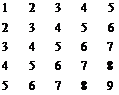
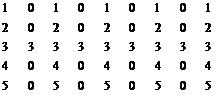
| I [8x8] (09, 29, 49, …, 89) | J [8x8] (10, 30, 50, …, 90) |
| 
|
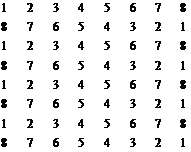
| K [5x5] (11, 31, 51, …, 91) | L [5x9] (12, 32, 52, …, 92) |
| 
|
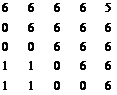
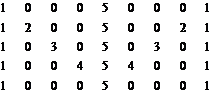
| M [5x5] (13, 33, 53, …, 93) | N [5x9] (14, 34, 54, …, 94) |
| 
|
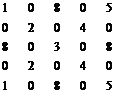
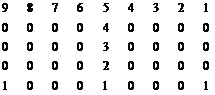
| O [8x8] (15, 35, 55, …, 95) | P [8x8] (16, 36, 56, …, 96) |
| 
|
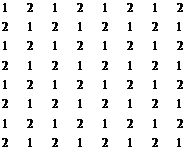
| R [8x8] (17, 37, 57, …, 97) | S [8x8] (18, 38, 58, …, 98) |
| 
|
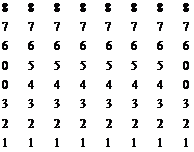
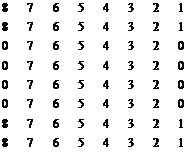
| T [8x8] (19, 39, 59, …, 99) | U [8x8] (20, 40, 60, …, 100) |
| 
|
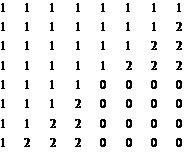
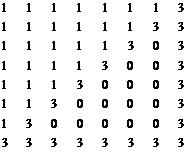
Задание № 3
Найти максимальное и минимальное значения функции y=F(x), а также соответствующие значения аргумента X при изменении аргумента X от Xн до Xк с шагом h, используя подпрограмму-функцию для вычисления функции F(x).
 Последняя цифра номера зачетной книжки
|
| N | Y=F(x) |
| 0 |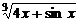 
|
| 1 | 2x +20,5x |
| 2 | cos(4,9 – x)1,5 |
| 3 | sin3 (2,5 + x) |
| 4 | cos (4 / x)2 |
| 5 | 12 / sin (1,6 +x) |
| 6 | 0,7 ln(5x2) |
| 7 | (4,6 – 3x)3 |
| 8 | 0,1 lg (2x +12) |
| 9 |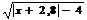 
|
| Предпоследняя цифра номера зачетной книжки |
| N | Начальное значение аргумента Хн | Конечное значение аргумента Хк | Шаг изменения аргумента h |
| 0 | -5 | 5 | 1 |
| 1 | -3 | 3 | 0,6 |
| 2 | 4 | 8 | 0,4 |
| 3 | -2 | 6 | 0,8 |
| 4 | 2,4 | 4 | 0,2 |
| 5 | -2,5 | 2,5 | 0,25 |
| 6 | 3 | 9 | 0,3 |
| 7 | -4 | -2 | 0,1 |
| 8 | 1 | 5 | 0,2 |
| 9 | -5 | 0 | 0,5 |
