Производная и дифференциал.

Элементарная математика.

Греческие буквы:

a – alpha;

β – beta;

γ – gamma;

δ – delta;

ξ – epsilon;

τ – theta;

λ – lambda;

χ – xi;

π – pi;

σ – sigma;

ψ – psi;

ω – omega.

 

Элементарные действия:

«+» – сложение;

«–» – вычитание;

«*» – произведение;

«/» – деление;

«^» – степень.

 

Числа

Infinity – бесконечность;

ехр – экспонента;

abs – модуль функции;

sqrt – корень;

log – логарифм;

ln – натуральный логарифм числа.

 

Элементарные преобразования:

subs – функция подстановки;

evalf – вычисление числовых выражений;

solve – вычисление корней выражения;

piecewise – задание системы с ограничением по х;

simplifi – упростить;

combine – преобразовать степень или тригонометрическое выражение.

 

Пример 1.

Вычислить значение функции:

,

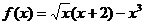 при .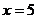

Решение.

> subs(x=5,sqrt(x)*(x+2)-x^3);

 

 

 

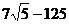
> evalf(7*5^(1/2)-125);

 

 

Ответ: .

 

 

Пример 2.

Решить уравнение:

.

 

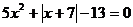Решение.

> solve(5*x^2+abs(x+7)-13=0);

 

,

 

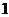
Сделаем проверку:

> subs(x=-6/5,5*x^2+abs(x+7)-13);

 

 

> subs(x=1,5*x^2+abs(x+7)-13);

 

 

Ответ: (-6/5,1).

 

Пример 3.

Задать функцию:

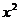
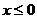
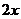
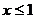
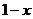
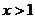
и найти её значения при .

 

Решение.

Зададим функцию:

> f:=piecewise(x<=0,x^2,x<=1,2*x,x>1,1-x);

 

x² x 0

                                    f:=     2*x x 1

1-x x>1

Найдём значение функции при х=0,5:

> subs(x=0.5,f);

.25  .5  0

1.0  .5  1

.5    1 <.5

 

Ответ: [0.25, 0.5 0],[1.0, 0.5 1],[0.5, 1 < 0.5].

 

Пример 4.

Упростить выражение:

.

Решение.

> simplify((a^3-b^3)/(a-b));

 

                                          

 

Ответ: .

 

Пример 5.

Преобразовать степень в данном выражении:

.

Решение.

> combine((x^(1/2))*x^(3/2));

 

                                                 

 

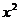
Ответ: .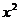

 

Упростить выражение

1. ;

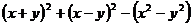2. ;

3. ;

4. ;

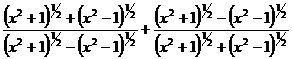5. ;

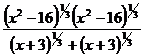6.  ;

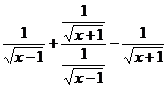7. ;

8. ;

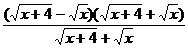9. ;

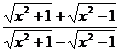10. .

 

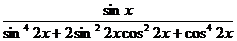Преобразовать степень

1. ;

2. ;

3. ;

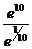4. ;

5. ;

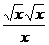6. ;

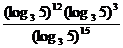7. ;

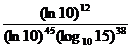8. ;

9. ;

10. .

 

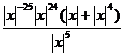Вычислить значение функции при , :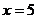

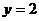1. ;

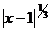2. ;

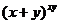3. ;

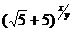4. ;

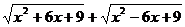5. ;

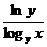6. ;

7. ;

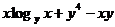8. ;

9. ;

10. .

 

Решить уравнения и неравенства

1. ;

2. ;

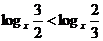3. ;

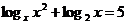4. ;

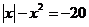5. ;

6. ;

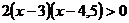7. ;

8. ;

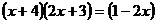9. ;

10. .

 

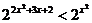Линейная алгебра.

Запуск пакета

> with(linalg);

[BlockDiagonal, GramSchmidt, JordanBlock, LUdecomp, QRdecomp,

Wronskian, addcol, addrow, adj, adjoint, angle, augment, backsub,

band, basis, bezout, blockmatrix, charmat, charpoly, cholesky,

col, coldim, colspace, colspan, companion, concat, cond, copyinto,

crossprod, curl, definite, delcols, delrows, det, diag, diverge,

dotprod, eigenvals, eigenvalues, eigenvectors, eigenvects,

entermatrix, equal, exponential, extend, ffgausselim, fibonacci,

forwardsub, frobenius, gausselim, gaussjord, geneqns, genmatrix,

grad, hadamard, hermite, hessian, hilbert, htranspose, ihermite,

indexfunc, innerprod, intbasis, inverse, ismith, issimilar,

iszero, jacobian, jordan, kernel, laplacian, leastsqrs, linsolve,

matadd, matrix, minor, minpoly, mulcol, mulrow, multiply, norm,

normalize, nullspace, orthog, permanent, pivot, potential,

randmatrix, randvector, rank, ratform, row, rowdim, rowspace,

rowspan, rref, scalarmul, singularvals, smith, stack, submatrix,

subvector, sumbasis, swapcol, swaprow, sylvester, toeplitz, trace,

transpose, vandermonde, vecpotent, vectdim, vector, wronskian]

 

matrix – задание матрицы;

vector – задание вектора;

type – проверка принадлежности к матрицам и векторам;

col – столбец матрицы с заданным номером;

coldim – количество столбцов в матрице;

row – строка матрицы с заданным номером;

rowdim – количество строк в матрице;

det – определитель матрицы;

eigenvals – собственные числа матрицы;

eigenvectors – собственные векторы матрицы;

inverse – обратная матрица;

multiply – произведение матриц;

evalm – произведение, сложение и вычитание матриц;

rank – ранг матрицы;

transpose – транспонирование матрицы; 

crossprod – векторное произведение векторов;

dotprod – скалярное произведение векторов;

angle – величина угла между векторами;

genmatrix – матрица системы.

 

Пример 1.

Решить систему уравнений:

,

,

,

.

 

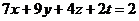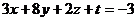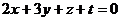Решение:

Задаем систему (отсутствие знака «=» означает равенство выражения нулю)

> F:=[7*X+9*Y+4*Z+2*T=2,2*X-2*Y+Z-T=6,3*X+8*Y+2*Z+T=-3,2*X+3*Y+Z+T];

 

F:= [7 X + 9 Y + 4 Z + 2 T = 2, 2 X - 2 Y + Z - T = 6, 3 X + 8 Y + 2 Z + T = -3, 2 X + 3 Y + Z + T]

 

x,y,z.t - набор букв, которые принимаются за неизвестные для данной матрицы

> v:=[X,Y,Z,T];

 

v:= [X, Y, Z, T]

 

задаём матрицу системы:

> a:=genmatrix(F,v);

 

a

 

находим определитель матрицы a:

> o:=det(a);

 

o:= 5

 

вводим остальные матрицы и находим их определители:

> A:=matrix([[7,9,4,2],[2,-2,1,6],[3,8,2,-3],[2,3,1,0]]);

 

A:=

 

 

> Ad:=det(A);

 

Ad:= -5

 

> B:=matrix([[7,9,2,2],[2,-2,-1,6],[3,8,1,-3],[2,3,1,0]]);

 

B:=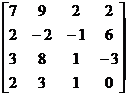

 

> Bd:=det(B);

 

Bd:= 7

 

> C:=matrix([[7,4,2,2],[2,1,-1,6],[3,2,1,-3],[2,1,1,0]]);

 

C:=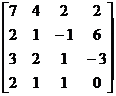

 

> Cd:=det(C);

 

Cd:= -4

 

> E:=matrix([[9,4,2,2],[-2,1,-1,6],[8,2,1,-3],[3,1,1,0]]);

 

 

E:=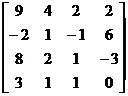

   

> Ed:=det(E);

 

Ed:= -12

 

> A1:=o/Ad;

 

A1:= -1

 

> B1:=o/Bd;

 

B1:= 5/7

 

> C1:=o/Cd;

 

C1:= -5/4

 

> E1:=o/Ed;

 

E1:= -5/12

                               

 

Ответ: x=-5/12, y=-5/4, z=5/7, t=-1.

 

Пример 2.

Выполнить действия с матрицами:

   

      

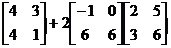
Решение.

Введем матрицы:

> A1:=matrix(2,2,[4,3,4,1]);

 

A1:=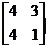

 

> A2:=matrix(2,2,[-1,0,6,6]);

 

A2:=  

 

> A3:=matrix([[2,5],[3,6]]);

 

A3:=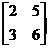

 

найдем произведение матрица А2 на число 2:

> B:=evalm(2*A2);

 

B:=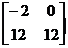  

 

Найдем произведение матриц В и А3:

> C:=evalm(B&*A3);

C:=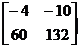

 

Найдём сумму матриц С и А1:

> F:=evalm(C+A1);

 

 

F:=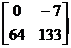

 

Проверим F на принадлежность к матрицам:

> type(F,matrix);

 

true

 

Ответ: .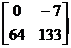

 

Пример 3.

Даны векторы

 А1 =(5,9,1) и А2 = (1,9,5)

Найти их векторное и скалярное произведение и найти угол между векторами А1 и А2.

 

Решение.

Зададим векторы А1 и А2

> А1:=vector([5,9,1]);

 

А1:= [5, 9, 1]

 

> А2:=vector(3,[1,9,5]);

 

А2:= [1, 9, 5]

 

Найдём векторное произведение:

> V:=crossprod(А1,А2);

 

V:= [36, -24, 36]

 

Скалярное поизведение векторов:

> S:=dotprod(A1,A2);

 

S:= 91

 

Величина угла между векторами:

> angle(A1,A2);

 

 

Пример 4.

Дана матрица:

А=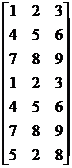     

 

 определить количество строк в матрице, показать 4 строку, найти обратную матрицу к матрице А и транспонировать ее.

 

Решение.

Задаем матрицу А:

C:=matrix([[1,2,3],[4,5,6],[7,8,9], [1,2,3],[4,5,6],[7,8,9],[5,2,8]]);

 

А:=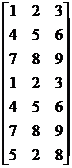

 

Определяем количество строк в матрице А:

> rowdim(A);

 

7

 

Покажем 4 строку:

> row(A,4);

 

[1,2,3]

 

Найдём обратную матрицу к матрице А:

> В:=inverse(A);

 

В:=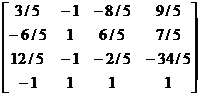

 

Транспонируем матрицу В:

> transpose(В);

 

 

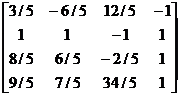
1                                              

 

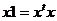
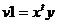
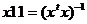
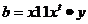
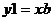
Графы

Запуск пакета

> with(networks);

[acycpoly, addedge, addvertex, adjacency, allpairs, ancestor,

arrivals, bicomponents, charpoly, chrompoly, complement, complete,

components, connect, connectivity, contract, countcuts,

counttrees, cube, cycle, cyclebase, daughter, degreeseq, delete,

departures, diameter, dinic, djspantree, dodecahedron, draw,

duplicate, edges, ends, eweight, flow, flowpoly, fundcyc,

getlabel, girth, graph, graphical, gsimp, gunion, head,

icosahedron, incidence, incident, indegree, induce, isplanar,

maxdegree, mincut, mindegree, neighbors, new, octahedron,

outdegree, path, petersen, random, rank, rankpoly, shortpathtree,

show, shrink, span, spanpoly, spantree, tail, tetrahedron,

tuttepoly, vdegree, vertices, void, vweight]

new – ввод нового графа;

addvertex – задача вершин графа;

connect – соединение вершин графа;

edges – края графа;

vertices – вершины графа;

draw – построение графа;

complete – ввод полного графа;

vdegree – определение степени вершины графа;

indegree – определение полу степени захода вершины графа;

outdegree – определение полу степени исхода вершины графа;

maxdegree – определение максимальной степени вершин графа;

delete – удаление вершин графа;

incidence – матрица инцидентности;

countcuts – минимальное число разрядов графа;

adjacency – матрица смежности.

 

Пример 1.

Построить граф G с вершинами 1,3,4,6; соединив 1 и 3 с 4 и 6,показав края графа и вершины, построить матрицу смежности и инцидентности.

 

Решение.

Задаём граф G:

> new(G):

задаём вершины данного графа:

> addvertex({1,3,4,6},G);

 

1, 3, 4, 6

 

соединяем 1 и 3 вершины с 4 и 6:

> connect({1,3},{4,6},G);

 

e1, e2, e3, e4

 

показываем края графа:

> edges(G);

 

{e4, e2, e1, e3}

 

показываем вершины графа:

> vertices(G);

 

{1, 3, 4, 6}

строим граф G:

> draw(G);

 

строим матрицу смежности:

> S:=adjacency(G);

 

S:=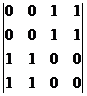

 

 

Строим матрицу инцидентности:

> Y:=incidence(G);

 

Y:=

Пример 2.

Построить полный граф с 6 вершинами, удалить 1 и 5 вершины, построить получившейся граф, определить полу степень захода вершины 6 и максимальную степень вершин.

 

Решение.

  Строим полный граф с 6 вершинами:

> G2:=complete(6):

 

> draw(G2);

 

удаляем 1 и 5 вершины:

> delete({1,5},G2):

 

строим получившейся граф:

> draw(G2);

находим полу степень захода вершины 6:

> indegree(6,G2);

 

0

находим максимальную степень вершин графа:

> maxdegree(G2);

 

3

Графики

Запуск пакета

> with(plots);

[animate, animate3d, changecoords, complexplot, complexplot3d,

conformal, contourplot, contourplot3d, coordplot, coordplot3d,

cylinderplot, densityplot, display, display3d, fieldplot,

fieldplot3d, gradplot, gradplot3d, implicitplot, implicitplot3d,

inequal, listcontplot, listcontplot3d, listdensityplot, listplot,

listplot3d, loglogplot, logplot, matrixplot, odeplot, pareto,

pointplot, pointplot3d, polarplot, polygonplot, polygonplot3d,

polyhedraplot, replot, rootlocus, semilogplot, setoptions,

setoptions3d, spacecurve, sparsematrixplot, sphereplot, surfdata,

textplot, textplot3d, tubeplot]

 

p lot – построение графика в декартовой системе координат, с обязательным указанием диапазона по горизонтальной оси (Ох);

color – указание цвета графика, в данной программе имеется 25 оттенков цветов;

 thickness – указание толщины линии, толщина задается от 0 до 15;

style – указание стиля графика, он может быть: point, line;

title – надпись на графике;

coords=polar – кривая заданная в полярных координатах;   

solve – нахождение абсцисс точек пересечения графиков функций;

plot3d – график в пространстве;

axes – оси;

inequal – построение замкнутой области;

optionsfeasible – цвет внутренней области замкнутого графика;

optionsexcluded – цвет внешней области замкнутого графика;

optionsclosed – цвет прямых, ограничивающих область, если она замкнутая.

Пример1.

Построить график функции .

 

Решение.

Строим график функции  с указанием диапазона по оси (Ох):

> plot(sin(x),x=-5..5);

 

Пример 2.

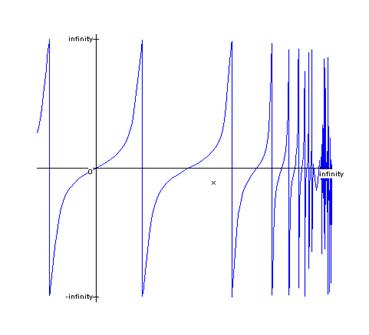
Построить график функции , , цвет графика - синий.

 

Решение.

Строим график функции .

> plot(tan(x),x=-2...infinity,color=blue);

 

Пример 3.

Построить график функции 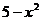, , 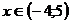цвет графика – зелёный, толщина лини – 20, стиль – точка и подписать график - парабола.

 

Решение.

Строим график функции .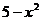

> plot(5-x^2,x=-4..5,y=-5..5,color=green,thickness=20,style=point,title='porabola');

 

Пример 4.

Построить график функции в полярных координатах , цвет графика – чёрный, толщина лини – 10, стиль – точка.

 

Решение.

Строим график функции .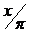

> plot(x/Pi,x=0..2*Pi,color=blak,thickness=10,style=point,coords=polar);

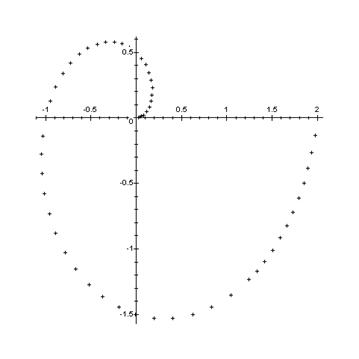
Пример 5.

Построить графики функций 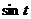, , 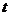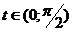; 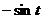, , 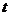; 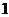, , 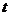 в полярных координатах.

 

Решение.

Строим графики функций:

> plot({[sin(t),t,t=0..Pi/2],[-sin(t),t,t=Pi..3*Pi/2],[1,t,t=0..2*Pi]},coords=polar); 

Пример 6.

Построить графики функци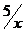й  и 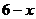, , 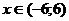, 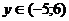найти абсциссы точек пересечения графиков функций.

 

Решение.

Строим графики функций:

> plot([5/x,6-x],x=-6..6,y=-5..6);

находим абсциссы точек пересечения графиков функций:

> solve(5/x=6-x,x);

 

1, 5

Ответ: 1,5

 

Пример 7.

Построить графики функций в пространстве 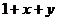 и , , 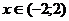, 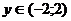зелёного цвета, оси расположены кубически.

 

Решение.

Строим графики функций:

> plot3d({1+x+y,1+x-y},x=-2..2,y=-2..2,axes=boxed,color=green);

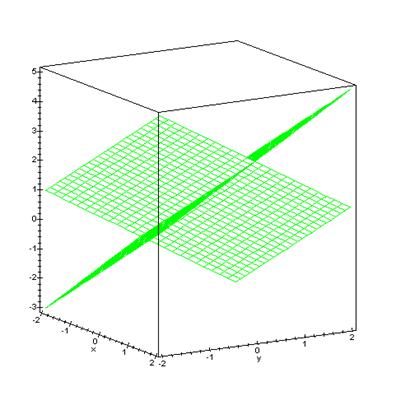
Пример 8.

Построить графики функций , , , ,  (-1;2), цвет внутренней области графика – красный, цвет внешней области графика – зелёный, цвет линий – синий, толщина линии - 6.

 

Решение.

Строим графики функций:

> inequal({x+y<=1,x>=0,y>=0},x=-1..2,y=-1..2,optionsfeasible=(color=red),optionsexcluded=(color=green),optionsclosed=(color=blue,thickness=6));

Построить графики функций, цвет графика – зелёный, стиль графика - точка.

1. ,  ;  

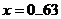2. , ;

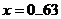3. , ;

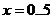4. ;

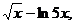
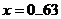5. , ;

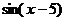6. , ;

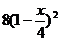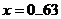7. , ;

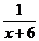8. , ;

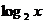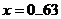9. , ;

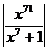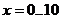10. , .

 

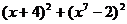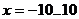Производная и дифференциал.

restart – аналитическое выражение функции;

diff – нахождение производной.

 

Пример 1.

Вычислить производную:

 

Решение.

Набираем аналитическое выражение данной функции:

> restart:((x^2-1)/(x^2+1))^4;

 

 

Находим производную:

> R0:=diff(((x^2-1)/(x^2+1))^4,x);

 

 

 

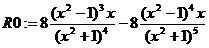
Ответ: .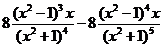

Пример 2.

Вычислить производную в заданной точке:

.

 

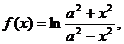
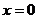Решение.

Набираем аналитическое выражение данной функции:

> restart:ln((a^2+x^2)/(a^2-x^2));

                                

 

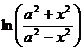
Находим производную:

> R0:=diff(ln((5+x^2)/(6-x^2)),x);

 

 

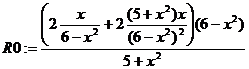
Подставляем x=0 и вычисляем результат:

> subs(x=0,R0);

0

 

Ответ: 0.

 

Пример 3.

Вычислить производную третьего порядка:

;

 

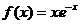Решение.

Находим производную:

> R0:=diff(x*exp^(-x),x$3);

 

R0:= 3exp^(-х)ln(exp)² -x exp^(-х)ln(exp)³

 

Ответ: 3exp^(-х)ln(exp)² -x exp^(-х)ln(exp)³.