Статистическая обработка экспериментальных данных

1. Предварительная математическая обработка статистических данных

После получения результатов эксперимента для дальнейшего их анализа проводится упорядочение данных, их графическое представление и расчет основных числовых характеристик.

Наблюдаемые значения исследуемого признака Х называют вариантами и обозначают , числа их наблюдений называют частотами и обозначают 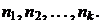 Общее число наблюдений называют объёмом выборки и обозначают n,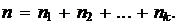

Последовательность вариант, записанных в возрастающем порядке, называется вариационным рядом. К характеристикам вариационного ряда относятся:

1) Размах варьирования R — это разность между наибольшим 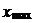 и наименьшим  значениями, ;

2) Мода Мо — это варианта, имеющая наибольшую частоту;

3) Медиана Ме — это варианта, делящая вариационный ряд пополам по числу вариант.

Статистическим распределением выборки называют множество вариант и соответствующих им частот. Обычно статистическое распреде-ление выборки представляют в виде таблицы:

			…
			…

 

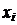
Эмпирической функцией распределения называется числовая функция , определяющая относительную частоту события  Она вычисляется по формуле:

                                    (1)

где   — сумма частот вариант, значения которых меньше х, n — объём выборки.

 является неубывающей функцией, значения которой принадлежат отрезку 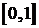.  служит оценкой теоретической функции распределения , определяющей вероятность события

Основными графическими формами представления данных наблюдений являются полигон частот и гистограмма.

Полигоном частот называется ломаная линия, звенья которой соединяют точки с координатами , , …, .

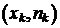Гистограммой называется ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат интервалы одинаковой длины h, а высотами — плотности интервальных частот .

Основными характеристиками выборки являются:

1) Выборочная средняя , вычисляется по формуле:

.                                  (2)

2) Выборочная дисперсия 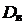, вычисляется по формуле:

.                            (3)

3) Исправленная дисперсия , вычисляется по формуле:

                                        (4)

4) Выборочное среднее квадратическое отклонение 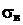, вычисляется по формуле:

                                      (5)

5) Исправленное среднее квадратическое отклонение s, вычисляется по   формуле:

                                         (6)

6) Коэффициент вариации V, вычисляется по формуле:

.                                     (7)

    Перечисленные характеристики относятся к точечным оценкам, при малых объёмах выборки предпочтительнее пользоваться интервальными оценками.

    Доверительным интервалом для параметра , точечной оценкой которого является , называют интервал , содержащий с заданной вероятностью  значение параметра ,  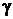называют надежностью оценки.

    Например, в случае нормально распределённой случайной величины доверительный интервал для среднего значения при неизвестном параметре  определяется формулой:

                                 (8)

где t — критическая точка распределения Стьюдента с  степенями свободы для двусторонней области на уровне значимости определяется по таблицам, например в .

Пример. Статистическая обработка результатов измерений (вычисления выполнять с точностью до двух знаков после запятой)

Даны результаты измерений значений случайной величины Х. Составить статистическое распределение выборки и найти:

а) характеристики вариационного ряда: размах варьирования, моду, медиану;

б) эмпирическую функцию распределения и построить ее график;

в) построить полигон частот и гистограмму;

г) выборочную среднюю;

д) выборочную и исправленную дисперсии;

е) выборочное и исправленное средние квадратические отклонения              

(стандарт);

ж) коэффициент вариации (%);

з) доверительный интервал для среднего значения признака Х с надежностью 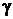=0,95;

12; 9; 16; 17; 10; 9; 15; 12; 15;16; 20; 18; 17; 9; 15; 9; 16; 9; 18; 16

    Составим статистическое распределение выборки. Для этого расположим варианты в порядке возрастания:

9; 9; 9; 9; 9; 10; 12; 12; 15; 15; 15; 16; 16; 16; 16; 17; 17; 18; 18; 20

и подсчитаем числа наблюдений каждой варианты — частоты. Получим:

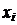
	9	10	12	15	16	17	18	20
	5	1	2	3	4	2	2	1

а) Размах варьирования  мода Мо =9; объём выборки n =20, поэтому середина вариационного ряда находится между 10-й и 11-й вариантами в упорядоченном вариационном ряду, и медиана вычисляется как их среднее арифметическое, Ме = (15+15)/2=15.

б) Эмпирическую функцию распределения найдём по формуле (1):

; 

;

;

  ;

  ;

  ;

  ;

  ;

         

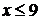
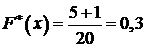    Построим график (рис. 1)

Рис. 1

в) Построим полигон частот (рис. 2). Для этого по оси  отложим наблюдаемые значения 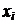, а по оси  частоты 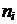. Отметим точки с координатами  и соединим их последовательно отрезками прямых.

Рис. 2

Для построения гистограммы разобьём интервал изменения x (9,20) на два интервала одинаковой длины h =5,5, подсчитаем интервальные частоты и плотности интервальных частот. Результаты внесём в таблицу 1.

Таблица 1

интервалы	Интервальные частоты	Плотности интервальных частот
	8	16/11
	12	24/11

Построим гистограмму (рис. 3).

Рис. 3

г) Вычислим выборочную среднюю по формуле (2):

.

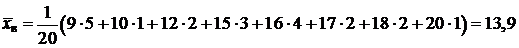д) Вычислим выборочную дисперсию формуле (3):

.

Исправленную дисперсию найдём по формуле (4):

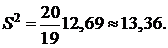
е) Выборочное и исправленное средние квадратические отклонения найдём по формулам (5) и (6):

ж) Коэффициент вариации вычислим по формуле (7):

з) Доверительный интервал для среднего значения признака Х найдём по формуле (8). Сначала по таблице [1] найдём критическую точку распределения Стьюдента с числом степеней свободы  и уровнем значимости  Получим t = 2,09 и подставим в формулу (8):

. После вычисления получим доверительный интервал для среднего значения

2. Вычисление ошибок прямых измерений

Ошибки измерений классифицируют как систематические, случайные и грубые промахи.

Систематическими называют такие ошибки, которые возникают из-за известных причин, действующих по определённым законам и, как правило, в определённом направлении. Их можно количественно определить и вносить в измерения соответствующие поправки.

Случайными называют такие ошибки, причины которых неизвестны и которые невозможно учесть заранее. Такие ошибки можно выразить несколькими способами. Часто пользуются понятием предельной ошибки 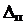, под которой понимают наибольшую случайную ошибку при пользовании исправным прибором при устранённых систематических ошибках. Она может быть определена из паспорта прибора или принята равной половине наименьшего деления шкалы прибора.

При определении величины случайных ошибок можно пользоваться статистической ошибкой, полученной неоднократными измерениями обработкой результатов методами математической статистики. В этом случае последовательность определения случайных ошибок следующая:

1) Прибором измеряют несколько раз (n раз) практически постоянную величину и находят её среднее арифметическое:

                                        (9)

2) Вычисляют исправленную дисперсию измеряемой величины:

                             (10)

и исправленное среднее квадратическое отклонение (стандарт):

                                         (11)

3) Тогда наибольшая возможная статистическая ошибка с

 вероятностью 99,73% в случае нормального закона распределения случайной величины будет:

                                        (12)

а относительная ошибка:

                            (13)

Пример. Определение погрешности прямых измерений (вычисления выполнять с точностью до двух знаков после запятой)

Даны результаты 10 равноточных измерений некоторой физической величины, проведенные без систематических ошибок. Вычислить

1) среднее значение измеряемой величины;

2) среднеквадратическую ошибку;

3) предельную относительную вероятностную ошибку, предполагая, что результаты измерений распределены нормально;

4) доверительный интервал для истинного значения измеряемой величины с надежностью =0,9.

Результаты измерений:

         7,94 8,45 9,09 8,71 8,39 9,37 9,26 8,68 8,28 8,39

1) Найдём среднее арифметическое по формуле (9):

2) Вычислим исправленную дисперсию по формуле (10) и исправленное среднее квадратическое отклонение по формуле (11):

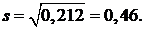 Итак, среднеквадратическая ошибка равна 0,46

3) Вычислим предельную ошибку по формуле (12) и относительную ошибку по формуле (13):

Окончательно результат измерений представляем в виде:

 относительная ошибка составляет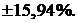

4) Доверительный интервал для среднего значения измеряемой величины найдём по формуле (8). Сначала по таблице [1] найдём критическую точку распределения Стьюдента с числом степеней свободы  и уровнем значимости  Получим t = 1,83 и подставим в формулу (8):

. После вычисления получим доверительный интервал для среднего значения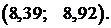

 

3. Вычисление ошибок косвенных измерений

В большинстве случаев в ходе эксперимента несколькими приборами измеряются несколько величин и для получения конечного результата эти измерения необходимо обработать, используя математические операции: сложения, умножения и т.д. Поэтому необходимо оценивать точность опыта в целом с помощью вычисления предельной и среднеквадратической ошибок опыта.

Правила вычисления предельной относительной ошибки опыта:

1. Ошибка суммы заключена между наибольшей и наименьшей из относительных ошибок слагаемых. Обычно учитывается или наибольшая ошибка или средняя арифметическая величина (в лабораторной работе будем пользоваться средней арифметической величиной).

2. Ошибка произведения или частного равна сумме относительных ошибок сомножителей или соответственно делимого и делителя.

3. Ошибка n -ой степени основания в n раз больше относительной ошибки основания.

Для вычисления среднеквадратической ошибки результата косвенных измерений необходимо обеспечить независимость результатов измерений. В этом случае среднеквадратическая ошибка вычисления величины W, являющейся функцией измеряемых прямо параметров x, y, z, … 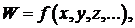 определяется формулой:

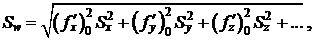                 (14)

где  — частные производные функции 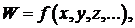 вычисленные при средних значениях параметров x, y, z, …,  — исправленные дисперсии соответственно x, y, z, ….

Пример. Определение погрешности косвенных измерений

    В результате многократных измерений были получены средние значения и среднеквадратические ошибки 3-х взаимно независимых параметров:

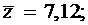
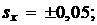
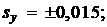
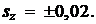
Найти:

а) предельную относительную ошибку измерений  и предельную относительную ошибку определения функции

б) среднее значение и среднеквадратическую ошибку определения функции

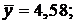
а) Найдём предельные относительные ошибки измерений x, y, z по формуле (13):

Предельную относительную ошибку определения функции

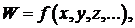 найдём по правилам вычисления предельной относительной ошибки опыта:

б) Вычислим среднее значение функции

Для вычисления среднеквадратической ошибки определения функции 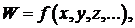  по формуле (14) найдём частные производные:

 

и вычислим их при средних значениях x, y, z:

Подставляя в формулу (14), получим:

4. Расчёт характеристик линейной регрессионной модели

Одним из эффективных методов установления взаимосвязей между факторами является корреляционно-регрессионный анализ.

    Задача корреляционно-регрессионного метода заключается в нахождении эмпирического уравнения, характеризующего связь результативного параметра Y c определённым входным фактором Х.

    В качестве формы связи Y и X широко используют линейную зависимость в силу её простоты в расчётах, а также в связи с тем, что к ней можно привести многие другие виды зависимости.

    Расчёт линейной регрессионной модели включает следующие этапы:

1. Расчёт теоретического уравнения линейной регрессии;

2. Оценка силы связи, расчёт коэффициента корреляции;

3. Оценка значимости коэффициента корреляции;

4. Оценка значимости коэффициентов уравнения регрессии;

5. Определение адекватности уравнения регрессии и доверительных границ.

Линейная регрессия Y на X имеет вид:

где α и β — параметры регрессии (β называется коэффициентом регрессии).

     Статистические оценки  и  параметров регрессии α и β выбираются таким образом, чтобы значения  вычисленные по формуле  были как можно ближе к эмпирическим значениям . В качестве меры близости выбирают сумму квадратов отклонений 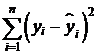. Метод нахождения параметров с помощью минимизации суммы квадратов отклонений эмпирических значений  от теоретических значений  в тех же точках называют методом наименьших квадратов. 

    Оптимальные значения параметров, полученные согласно этому методу, определяются формулами:

                  (15)

где и — средние значения X и Y, которые вычисляют по формулам:

                                      (16)

       Учитывая (15), запишем эмпирическую линию регрессии в виде:

                                           (17)

    Силу линейной корреляционной зависимости Y и X характеризует коэффициент корреляции r. Коэффициент r изменяется в пределах от  до 1. Чем ближе он к , тем сильнее линейная связь Y и X, в предельном случае, если , имеет место точная линейная функциональная зависимость Y от  X. Если , то Y и X не коррелируют. Оценкой коэффициента корреляции r служит выборочный коэффициент корреляции 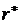, который вычисляется по формуле:

                         (18)                                                                                                                           

    Коэффициент корреляции определяемый по выборочным данным, может не совпадать с действительным значением, соответствующим генеральной совокупности. Для проверки статистической гипотезы о значимости выборочного коэффициента корреляции используют t -критерий Стьюдента, наблюдаемое значение которого вычисляется по формуле:

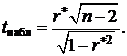                                  (19)                                                                                                                               

    Критическое значение t -критерия  для числа степеней свободы  и уровня значимости α находят по таблицам критических точек распределения Стьюдента [1]. Если , то предположение о нулевом значении коэффициента корреляции не подтверждается, и выборочный коэффициент корреляции значим. Если , то величина r  близка к нулю.  

       Для оценки параметров, входящих в уравнение регрессии (16), при решении практических задач можно ограничиться построением доверительных интервалов. Для заданной надёжности γ доверительные интервалы для параметров 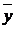 и β определяются формулами:

                           (20) 

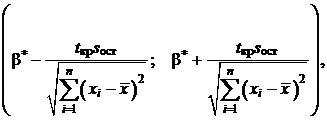             (21)    

где  — критическое значение  t -критерия для числа степеней свободы  и уровня значимости , которое находят по таблицам критических точек распределения Стьюдента [1], — квадратный корень из остаточной дисперсии , которая находится по формуле:

.                           (22)  

    После получения эмпирического уравнения регрессии, проверяют насколько оно соответствует результатам наблюдений. Для проверки гипотезы о значимости уравнения регрессии используют F -критерий Фишера, наблюдаемое значение которого вычисляют по формуле:

                                      (23)

где — исправленная дисперсия Y, которая вычисляется по формуле:

                               (24)

    Критическое значение F -критерия  для числа степеней свободы  и  и уровня значимости α находят по таблицам критических точек распределения Фишера-Снедекора [1]. Если , то гипотеза о незначимости уравнения регрессии не подтверждается, и уравнение соответствует результатам наблюдений. Если 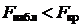, то полученное уравнение незначимо.

    Ещё одной характеристикой меры того, насколько эмпирическое уравнение хорошо описывает данную систему наблюдений, является коэффициент детерминации d, который вычисляется по формуле:

                                       (25)

       Чем ближе коэффициент d к единице, тем лучше описание.

    После того как модель построена, она используется для анализа и прогноза. Прогноз осуществляется подстановкой фактора  в уравнение (17). Получается точечная оценка :

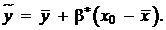                         (26)

 Доверительный интервал для прогнозируемого значения имеет вид:

(27)

где  — критическое значение t -критерия для числа степеней свободы  и уровня значимости , которое находят по таблицам критических точек распределения Стьюдента [1].

Пример. Построение модели линейной регрессии

         По данным наблюдений определить параметры линейного уравнения регрессии Y на X. Найти коэффициенты регрессии и корреляции проверить гипотезу о значимости выборочного коэффициента корреляции. Найти доверительные интервалы для параметров уравнения регрессии. Определить коэффициент детерминации. Проверить гипотезу о значимости полученного уравнения регрессии. Найти прогнозируемое моделью значение y при x = x ₀ и найти для него доверительный интервал. Уровень значимости   принять равным 0,05.  

X	73	85	102	115	122	126	134	147
Y	0,5	0,7	0,9	1,1	1,4	1,4	1,7	1,9

                     

    Для получения параметров уравнения регрессии составим таблицу. Таблица 2

73 85 102 115 122 126 134 147	0,5 0,7 0,9 1,1 1,4 1,4 1,7 1,9	-40 -28 -11 2 9 13 21 34	-0,7 -0,5 -0,3 -0,1 0,2 0,2 0,5 0,7	1600 784 121 4 81 169 441 1156	0,49 0,25 0,09 0,01 0,04 0,04 0,25 0,49	28               14 3,3 -0,2 1,8 2,6 10,5 23,8	0,43 0,661 0,998 1,239 1,373 1,450 1,604 1,854	0,0049 0,0015 0,0077 0,0193 0,0007 0,0025 0,0092 0,0021
904	9,6	0	0	4356	1,66	83,8		0,0479

    В последней строке таблицы приведены суммы столбцов, используемых в расчётах.

    Найдём средние значения X и Y по формуле (16):

    Вычислим коэффициент регрессии по формуле (15):

 и получим эмпирическое уравнение регрессии, подставляя  в (17):

                           (28)

    По формуле (28) вычислим теоретические значения  и заполним два последних столбца таблицы 2.

    Вычислим коэффициент корреляции по формуле (18):

 и проверим гипотезу о его значимости. Наблюдаемое значение критерия найдём по формуле (19):

 По таблице критических точек распределения Стьюдента [1] найдём критическую точку распределения Стьюдента с числом степеней свободы  и уровнем значимости  Получим  и сравним  и : следовательно, коэффициент корреляции значим, и Y и X связаны линейной корреляционной зависимостью.

    Для определения доверительных интервалов параметров уравнения линейной регрессии (28) найдём остаточную дисперсию по формуле (22):

Подставляя в формулу (20), получим доверительный интервал для  Вычисляя, получим интервальную оценку для с надёжностью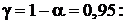

Доверительный интервал для  получим по формуле (21):

 Итак, интервальная оценка для параметра с надёжностью

    Проверим гипотезу о значимости полученного уравнения регрессии. Для вычисления наблюдаемого значения F -критерия найдём исправленную дисперсию Y по формуле (24):  Подставляя в формулу (23), получим:  По таблице критических точек распределения Фишера-Снедекора [1] для числа степеней свободы  и 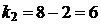 на уровне значимости найдём 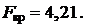 Сравнивая наблюдаемое и критическое значения F -критерия, получим  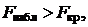следовательно, уравнение значимо.

     Для оценки адекватности линейной модели наблюдаемым значениям найдём также коэффициент детерминации по формуле (25):

 Этот результат истолковывается так: 97,1% изменчивости Y объясняется изменением фактора X, а на остальные случайные факторы приходится 2,9% изменчивости. Однако, этот вывод действителен только для рассматриваемого интервала значений X.

    Используем уравнение (28) для прогноза. При точечную оценку для y получим путём подстановки в формулу (28): 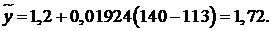 Доверительный интервал для получим по формуле (27):

Окончательно, интервальная оценка для  с надёжностью