Вычисляют выборочную дисперсию, характеризующую меру разброса опытных данных (xi; yi) вокруг значений регрессии, то есть дисперсию остатков
.
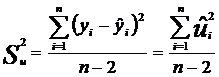Знаменатель показывает число степеней свободы. Оно определяется как разность между объемом выборки и числом параметров регрессии, подлежащих оценке. Стандартной ошибкой регрессии называется
.
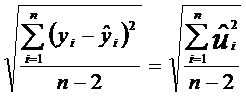Стандартная ошибка должна быть минимальна, это равносильно условию:
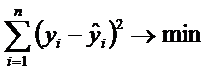. (1)
Геометрическая интерпретация формулы (1) следующая: сумма площадей заштрихованных квадратов должна быть наименьшей.
Пусть ŷi = b0 + b1x1; i = 1, 2, …, n; тогда
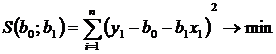и надо найти b0 и b1.
Для наличия экстремума S(b0; b1) необходимо выполнение равенств:
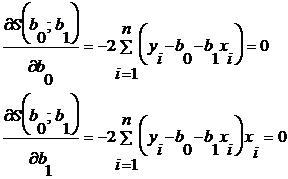(2)
Для вторых частных производных функции S(b0; b1) справедливы соотношения:
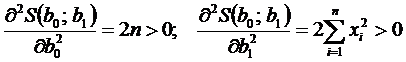
Существование минимума обеспечивается выполнением условия: 
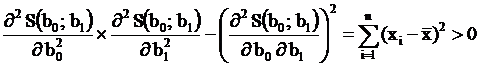
После преобразований уравнений (2) получаем систему двух уравнений первой степени (систему нормальных уравнений) относительно неизвестных b0 и b1:
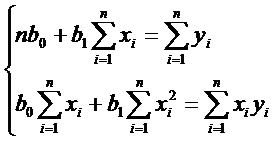(3)
Применяя к ней правило Крамера, получаем:
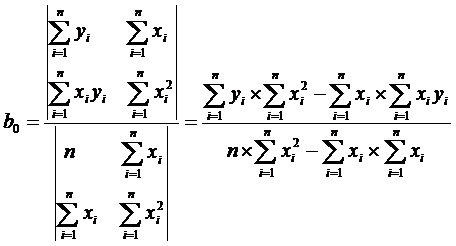
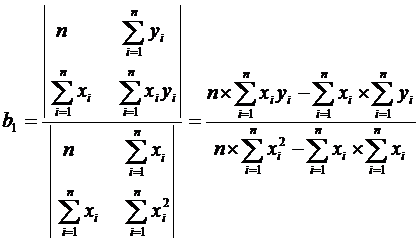
Получить b0 и b1 из уравнений (3) можно по-другому. Первое из уравнений системы почленно разделим на n. Тогда
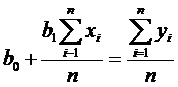; или
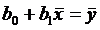, откуда 
;
; 
.
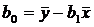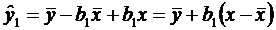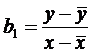Коэффициент регрессии b1 можно представить следующим образом:
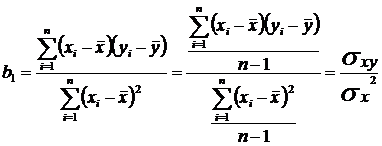, где
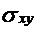- ковариация между переменными x и y, 
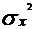- дисперсия переменной x.
Вычислим коэффициенты регрессии общей суммы налогового сбора (переменная y) на сумму поступлений налога на добавленную стоимость по несгруппированным данным:
| Время наблюдения | № наблюдения | y (общая сумма налогов и платежей в консолидированный бюджет РФ), млрд. руб. | x (общая сумма поступлений в консолидированный бюджет РФ по НДС), млрд. руб. | xi2 | yi2 | xiyi |
| январь | 1 | 38,9 | 13,4 | 179,56 | 1513,21 | 521,26 |
| февраль | 2 | 45,3 | 15,4 | 237,16 | 2052,09 | 697,62 |
| март | 3 | 61,1 | 16,7 | 278,89 | 3733,21 | 1020,37 |
| апрель | 4 | 70,4 | 16,2 | 262,44 | 4956,16 | 1140,48 |
| май | 5 | 63,8 | 13,0 | 169 | 4070,44 | 829,4 |
| июнь | 6 | 67,7 | 15,0 | 225 | 4583,29 | 1015,5 |
| июль | 7 | 70,6 | 20,8 | 432,64 | 4984,36 | 1468,48 |
| август | 8 | 78,9 | 16,4 | 268,96 | 6225,21 | 1293,96 |
| сентябрь | 9 | 73,2 | 17,4 | 302,76 | 5358,24 | 1273,68 |
| октябрь | 10 | 78,1 | 23,6 | 556,96 | 6099,61 | 1843,16 |
| ноябрь | 11 | 103,0 | 23,9 | 571,21 | 10609 | 2461,7 |
| декабрь | 12 | 133,4 | 34,4 | 1183,36 | 17795,56 | 4588,96 |
| Σ | 884,4 | 226,1 | 4667,94 | 71980,4 | 18154,6 |
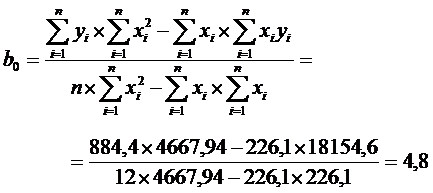
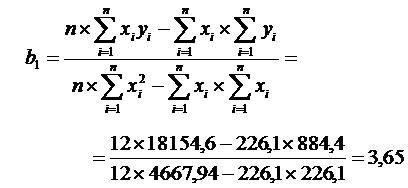
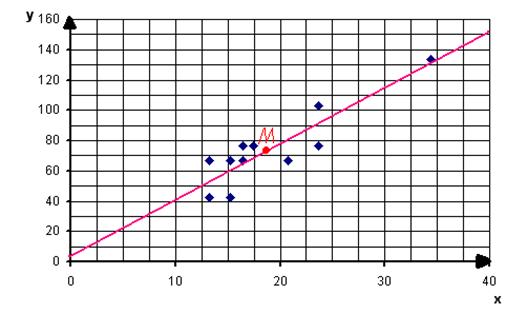График уравнения регрессии y на x выглядит следующим образом:
 |
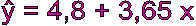Экономические явления обычно находятся во взаимодействии, то есть переменная y зависит от переменной x, и наоборот, переменная x зависит от переменной y. В этом случае говорят о логически обратимой регрессии. При переходе от одной зависимости к другой нельзя из уравнения
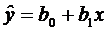
выразить x выразить через y, так как эмпирические точки лежат не на прямой, а подвержены рассеянию и фиксированному значению x может соответствовать несколько значений y и наоборот.
Уравнения регресси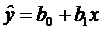и 
и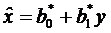 
не выводимы друг из друга. Они задают сопряженные регрессионные прямые.
Построим регрессию x на y для рассматриваемого нами примера.
;
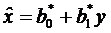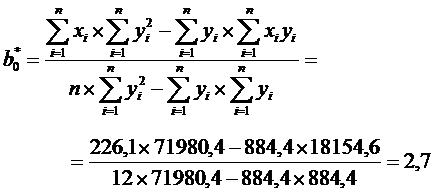
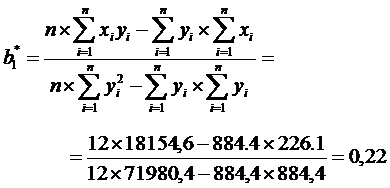
График регрессии x на y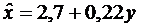 
будет выглядеть следующим образом:
 |
Совместим графики регрессии x на y и y на x:
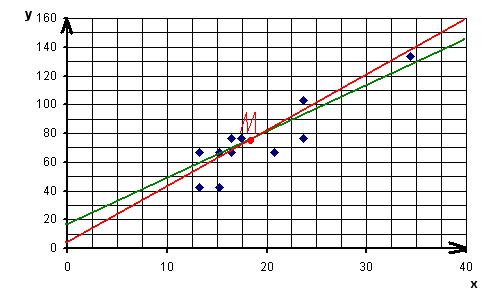
Регрессионные прямые образуют «ножницы». По величине раствора ножниц можно судить приблизительно о степени зависимости обеих переменных. Чем более раскрыты ножницы, тем слабее связь. Если обе прямые регрессии пересекаются под прямым углом, то эмпирические данные не позволяют подтвердить гипотезу о существовании зависимости между переменными. Если отсутствует регрессия x на y, то не существует также регрессии y на x, и наоборот. При b1 = 0 обязательно b1* = 0 и обратно.
