С помощью функции регрессии
количественно оценивается усредненная зависимость между исследуемыми переменными. Наблюдая за интересующей его зависимостью при сложном взаимодействии объясняющих переменных, исследователь с помощью регрессии отвечает на вопрос: какова была бы зависимость между следствием и выделенными существенными причинами, если бы прочие факторы не изменялись?
Результаты наблюдений можно представить в виде таблицы.
| № наблюдения | Переменные | |||||
| Зависимая | Объясняющие | |||||
| y | x1 | … | xk | … | xm | |
| 1 | y1 | x11 | … | x1k | … | x1m |
| 2 | y2 | x21 | … | x2k | … | x2m |
| … | … | … | … | … | … | … |
| i | yi | xi1 | … | xik | … | xim |
| … | … | … | … | … | … | … |
| n | yn | xn1 | … | xnk | … | xnm |
Каждый столбец этой таблицы представляет ряд наблюдений над одной переменной. Номер столбца k показывает номер соответствующей объясняющей переменной, номер строки i показывает номер наблюдения. Значения yi и xik являются эмпирическими или опытными данными.
Случайная переменная 
, характеризующая отклонение переменной y от средней величины ŷ, называется возмущающей переменной (латентной переменной) или возмущением. Значения u нельзя получить непосредственно. Значения возмущающей переменной u можно получить лишь после количественной оценки зависимости в виде функции регрессии. Вычисленные оценки û значений переменной u и называются остатками. Избранная функция регрессии должна отображать экономическую закономерность, поэтому перед построением функции регрессии необходимо провести качественный экономический анализ изучаемого явления, позволяющий вскрыть все сторонние связи изучаемого явления.
При анализе зависимости между двумя переменными (например, y и xk) по таблице можно построить в декартовой системе координат диаграмму рассеяния:
В результате действия побочных факторов
(x 1, x 2, …, xk -1, xk, xk +1, …, xm)
каждому фиксированному значению переменной xk может соответствовать несколько значений переменной y.
Диаграмма рассеяния позволяет произвести визуальный анализ эмпирических данных, по ней можно графическим путем определить функцию регрессии, которая обязательно должна проходить через точку 
- центр рассеяния, и которая должна по возможности хорошо отражать характер скопления точек.
Пример
Проанализируем зависимость (по месяцам) общей суммы налогов и платежей (переменная y) от поступлений по налогу на добавленную стоимость в 1999 г. по данным Министерства по налогам и сборам РФ.
| Время наблюдения | № наблюдения | y (общая сумма налогов и платежей в консолидированный бюджет РФ), млрд. руб. | x (общая сумма поступлений в консолидированный бюджет РФ по НДС), млрд. руб. |
| январь | 1 | 38,9 | 13,4 |
| февраль | 2 | 45,3 | 15,4 |
| март | 3 | 61,1 | 16,7 |
| апрель | 4 | 70,4 | 16,2 |
| май | 5 | 63,8 | 13,0 |
| июнь | 6 | 67,7 | 15,0 |
| июль | 7 | 70,6 | 20,8 |
| август | 8 | 78,9 | 16,4 |
| сентябрь | 9 | 73,2 | 17,4 |
| октябрь | 10 | 78,1 | 23,6 |
| ноябрь | 11 | 103,0 | 23,9 |
| декабрь | 12 | 133,4 | 34,4 |
| январь-декабрь | 884,4 | 226,1 | |
| 
|
Диаграмма рассеяния будет иметь следующий вид:
Линия регрессии y на x проходит через точку М(18,85; 73,7).
Метод частных средних
Среднее, связанное с определенными предположениями или вычисленное при определенных условиях, называется частным, условным или групповым средним. Частные средние переменных x и y вычисляются по формулам:
где 
- частное среднее переменной x для i –группы значений переменной y (значения переменной y разбиты q групп),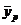 
- частное среднее переменной y для p -группы значений переменной x (значения переменной x разбиты на s групп); nj и np – число отдельных значений в группе j и группе p; 
Пример
| Время наблюю-дения | № наблюю-дения | y (общая сумма налогов и платежей в консолидированный бюджет РФ), млрд. руб. | № группы значений y | x (общая сумма поступлений в консолидированный бюджет РФ по НДС), млрд. руб. | № группы значений x |
| январь | 1 | 38,9 | 1 | 13,4 | 1 |
| февраль | 2 | 45,3 | 1 | 15,4 | 2 |
| март | 3 | 61,1 | 2 | 16,7 | 3 |
| апрель | 4 | 70,4 | 2 | 16,2 | 3 |
| май | 5 | 63,8 | 2 | 13,0 | 1 |
| июнь | 6 | 67,7 | 2 | 15,0 | 2 |
| июль | 7 | 70,6 | 2 | 20,8 | 5 |
| август | 8 | 78,9 | 3 | 16,4 | 3 |
| сентябрь | 9 | 73,2 | 3 | 17,4 | 4 |
| октябрь | 10 | 78,1 | 3 | 23,6 | 6 |
| ноябрь | 11 | 103,0 | 4 | 23,9 | 6 |
| декабрь | 12 | 133,4 | 5 | 34,4 | 7 |
Группировка значений переменной y построена так, что вариация значений переменной yi и yj из одной группы не превосходит 10.
Группировка значений переменной x построена так, что вариация значений переменной xi и xj из одной группы не превосходит 1.
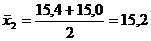
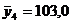
Представим полученные значения частных средних графически. Для этого из точек, соответствующих значениям переменной x, нужно восставить перпендикуляры к оси абсцисс и отложить их на значения 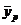. Вершины ординат нужно последовательно соединить прямолинейными отрезками, то есть прямое соединяем следующие точки:
М1(13,2; 42,1); М2(15,2; 42,1); М3(16,4; 66,7); М4(16,4; 66,7);
М5(13,2; 66,7); М6(15,2; 66,7); М7(20,8; 66,7); М8(16,4; 76,7);
М9(17,4; 76,7); М10(23,7; 76,7); М11(23,7; 103,0); М12(34,4; 133,4).
Эмпирическая линия регрессии y на x:
Эмпирическая линия регрессии x на y не совпадает с эмпирической линией регрессии y на x. Поэтому при изучении зависимости необходимо отмечать направление зависимости между изучаемыми переменными.
